
Задачи по Машиностроительной Гидравлике
Сборник Задач. Учебное пособие для машиностроительных вузов. УДК 621-82(075.8) ББК 30.123. Москва 2002 г.
И.И.Куколевский, Д.А.Бутаев, З.А.Калмыкова, Л.Г.Подвидз, К.Н.Попов, С.Н.Рождественский, Б.И.Яньшин

ЧАСТЬ 1. ГИДРОСТАТИКА
ГЛАВА 1.
ДАВЛЕНИЕ В ПОКОЯЩЕЙСЯ ЖИДКОСТИ
Задача 1.1
Цена - 80 руб. (pdf) - 100 руб. (word)
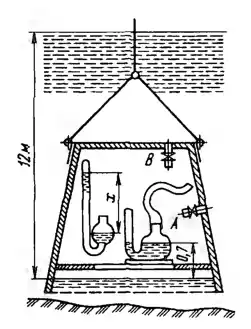
Рисунок 1.1
Каково показание х ртутного барометра, помещенного в водолазном колоколе, если поверхность воды (ρ = 1025 кг/м3) в колоколе на 12 м ниже уровня моря, а показание барометра на поверхности моря 750 мм. рт. ст.? Как установится ртуть в манометре с «постоянным» нулем, если манометр присоединить к крану А колокола? Как она установится, если манометр присоединить к крану В? Считать, что при измерениях воздух в соединительной трубке, ведущей к чашке прибора, отсутствует.
Задача 1.2
Цена - 80 руб. (pdf) - 100 руб. (word)
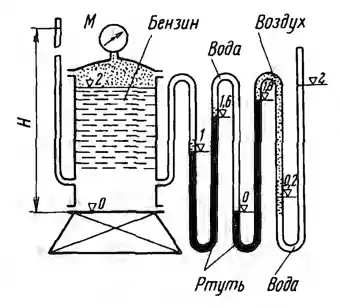
Рисунок 1.2
К резервуару, наполненному бензином (относительная плотность δ = 0,7), до высоты ∇2, присоединены три различных прибора для измерения давления. К крышке резервуара присоединен пружинный манометр, к боковым стенкам пьезометр и трехколенный манометр, наполненный ртутью (δ = 13,6), водой (δ = 1) и воздухом (δ = 0). Определить показания М манометра и Н пьезометра, если уровни жидкостей в трехколенном манометре расположились так, как показано на эскизе (отметки уровней даны в метрах).
Задача 1.3
Цена - 80 руб. (pdf) - 100 руб. (word)
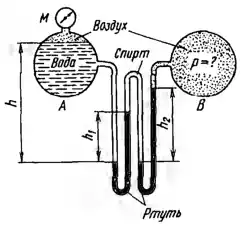
Рисунок 1.3
Найти давление воздуха р в резервуаре В, если избыточное давление на поверхности воды в резервуаре А равно рм = 25 кПа, разности уровней (δрт = 13,6) в двух коленном дифференциальном манометре h1 = 200 мм и h2 = 250 мм, а мениск ртути в левой трубке манометра ниже уровня воды на h = 0,7 м. Пространство между уровнями ртути в манометре заполнено спиртом (δс = 0,8).
Задача 1.4
Цена - 80 руб. (pdf) - 100 руб. (word)
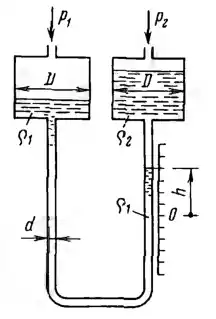
Рисунок 1.4
Двухжидкостный микроманометр состоит из U-образной трубки диаметром d = 5 мм, соединяющей чашки диаметрами D = 50 мм. Прибор наполнен несмешивающимися жидкостями с близкими удельными весами -водным раствором этилового спирта (ρ1 = 870 кг/м3) и керосином (ρ2 = 830 кг/м3).
1) Установить связь между измеряемой микроманометром разностью давлений газа Δр = р1−р2 и смещением h мениска раздела жидкостей от его начального положения, отвечающего р = 0. Определить р при h = 280 мм. 2) Указать, во сколько раз уменьшатся показания прибора при данном р, если в приборе будут отсутствовать чашки.
Задача 1.5
Цена - 80 руб. (pdf) - 100 руб. (word)
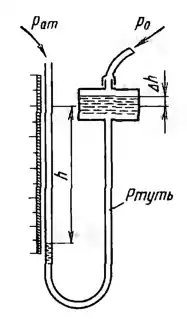
Рисунок 1.5
Использование шкалы с постоянным нулем при измерении давлений чашечным ртутным манометром или вакуумметром вносит погрешность в результат измерения. Для нахождения истинной величины давления в показание h прибора необходимо вносить поправку на смешение dh уровня ртути в чашке. Пренебрегая влиянием капиллярности, определить: 1) Какова погрешность, вызываемая смещением уровня ртути в чашке при диаметрах чашки D = 60 мм и трубки d = 6 мм? 2) Каким образом проградуировать шкалу прибора, чтобы отсчет по шкале соответствовал истинному давлению?
Задача 1.6
Цена - 80 руб. (pdf) - 100 руб. (word)
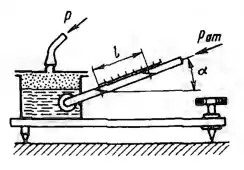
Рисунок 1.6
Применение для измерения малых избыточных давлений в газах спиртового чашечного микроманометра с наклонной шкалой значительно увеличивает точность измерений.
1. Принимая точность отсчета невооруженным глазом по шкале 0,5 мм, определить, под каким углом к горизонту нужно расположить трубку прибора, чтобы при измерении давления в пределах 1 ÷ 2 кПа погрешность измерения не превышала +-0,2%. Относительный вес спирта δс = 0,8.
2. Какова максимальная погрешность при измерении того же давления ртутным (δ = 13,6) чашечным манометром с вертикальной шкалой? Диаметры чашек считать настолько большими, чтобы можно было пренебречь поправкой на смещение уровня в них.
Задача 1.7
Цена - 80 руб. (pdf) - 100 руб. (word)
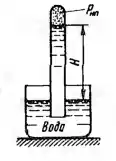
Рисунок 1.7
На какой высоте H установится вода в трубке, первоначально заполненной водой, а потом опрокинутой и погруженной открытым концом под уровень воды, если атмосферное давление 98 кПа и температура воды 4°С? Как изменится высота Н, если температура повысится до 20 °С, до 80 °С? Величины давления насыщенных паров воды и ее удельного веса заданы ниже.
|
t, ℃ |
4 |
20 |
80 |
|
Pнп, кПа |
0,618 |
2,31 |
47,4 |
|
ρ, кг/м3 |
1000 |
998,2 |
971,8 |
Задача 1.8
Цена - 80 руб. (pdf) - 100 руб. (word)
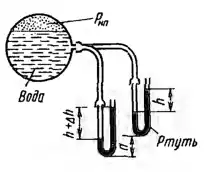
Рисунок 1.8
Давление на поверхности воды в резервуаре измеряется ртутным U-образным манометром. Как изменится показание (h мм) манометра, если его переместить вниз на а мм при неизменном давлении и практически неизменном ее уровне?
Задача 1.9
Цена - 80 руб. (pdf) - 100 руб. (word)
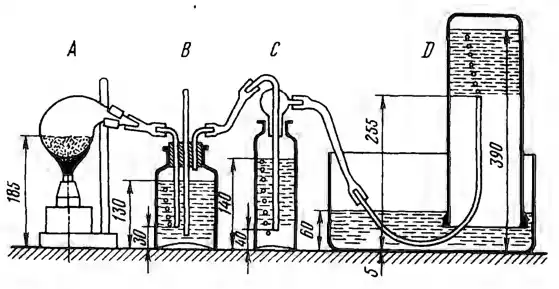
Рисунок 1.9
Выделившийся вследствие химической реакции газ из реторты А направляется последовательно в сосуды В к С, наполненные промывными растворами (δВ = 1,03 и δС = 1,05), и в сборник В, наполненный водой. Определить давление в реторте А, сосудах В и С и в сборнике D при указанных на чертеже размерах (в мм). Сопротивлением проходу газа по трубкам пренебречь.
Задача 1.8
Цена - 80 руб. (pdf) - 100 руб. (word)
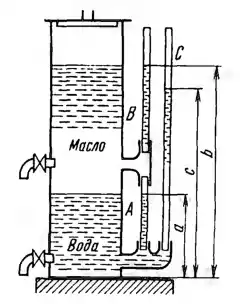
Рисунок 1.10
В цилиндрическом отстойнике поверхность раздела между маслом и осевшей водой определяется по стеклу А, а верхний уровень масла - по стеклу В. Определить:
1) Определить плотность масла, если а = 0,2 м, b = 1,4 м, а уровень воды в дополнительной трубке С установился на высоте с = 1,2 м? 2) Каковы будут высоты уровней а, b, с в трубках, если при тех же объемах воды и масла в отстойнике над маслом будет избыточное давление P = 10 кПа? Объемом жидкости в трубках пренебречь.
Задача 1.11
Цена - 80 руб. (pdf) - 100 руб. (word)
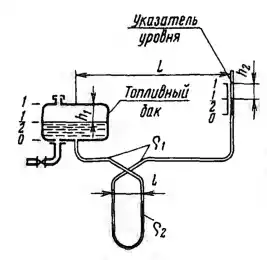
Рисунок 1.11
Указатель уровня топливного бака выполнен в виде U-образной трубки с перекрещивающимися ветвями заполненными топливом плотностью ρ1 и несмешивающейся с топливом жидкостью плотностью ρ2 (ρ2 > ρ1). 1. Установить зависимость между понижением h1 уровня в баке и понижением h2 уровня в открытой ветви трубки от их начальных положений, соответствующих начальному заполнению бака. 2. При каком соотношении длин l/L наклон системы в вертикальной плоскости не будет влиять на положение уровня в трубке и, следовательно, не будет искажать показаний прибора?
Задача 1.12
Цена - 80 руб. (pdf) - 100 руб. (word)
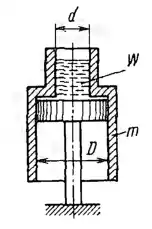
Рисунок 1.12
Покоящийся на неподвижном поршне и открытый сверху и снизу сосуд массой m =16 кг состоит из двух цилиндрических частей, внутренние диаметры которых равны D = 0,5 м и d = 0,3 м. Определить, какой минимальный объем W воды должен быть налит в верхнюю часть сосуда, чтобы сосуд всплыл над поршнем. Трением сосуда о поршень пренебречь.
Задача 1.13
Цена - 80 руб. (pdf) - 100 руб. (word)
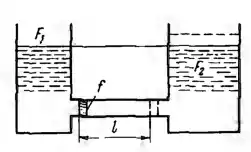
Рисунок 1.13
Определить работу, затрачиваемую на перемещение поршня площадью f на расстояние l в трубопроводе, соединяющем два резервуара площадями F1 и F2, заполненные при начальном положении поршня до одной и той же высоты жидкостью удельного веса γ. Трением поршня о стенки трубопровода пренебречь.
Задача 1.14
Цена - 80 руб. (pdf) - 100 руб. (word)
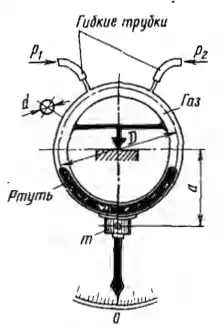
Рисунок 1.14
Определить, на какой угол повернется кольцевой манометр, имеющий диаметр трубки d = 20 мм. и средний диаметр кольца D = 200 мм, если величины давления воздуха, подводимого к ветвям, равны P1 = 90 кПа и P2 = 80 кПа, масса груза m = 0,535 кг (вес груза G = 5,25 Н) и его плечо относительно оси вращения а = 120 мм.
Задача 1.15
Цена - 80 руб. (pdf) - 100 руб. (word)
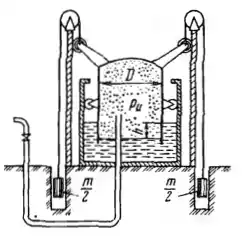
Рисунок 1.15
Тонкостенный газгольдер, имеющий диаметр D = 12,5 м и массу M = 45∙103 кг наполнен светильным газом. Пренебрегая трением, определить массу грузов m (Q = mg), необходимый для поддержания в газгольдере давления pи = 2 кПа, и образующуюся при этом разность h уровней воды в резервуаре и газгольдере. Каково предельное значение для данного газгольдера?
Задача 1.16
Цена - 80 руб. (pdf) - 100 руб. (word)
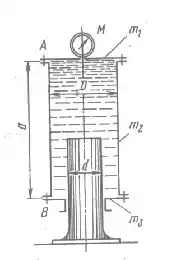
Рисунок 1.16
Цилиндрический сосуд диаметром D = 0,2 м и высотой а = 0,4 м, заполненный водой, опирается на плунжер диаметром d = 0,1 м. Определить показание манометра М и усилия в болтовых группах А и В, если вес верхней крышки сосуда равен m1 = 300 кг, вес цилиндрической части сосуда m2 = 150 кг, вес нижней крышки сосуда m3 = 120 кг. Каким может быть взят минимальный диаметр плунжера, если наибольшее допускаемое давление M = 3 МПа? Указание. Одним из возможных способов расчета давления М является рассмотрение условия равновесия сосуда под действием его собственного веса и приложенных к его внутренней поверхности сил избыточного давления жидкости, величины которых зависят от давления М.
Задача 1.17
Цена - 80 руб. (pdf) - 100 руб. (word)
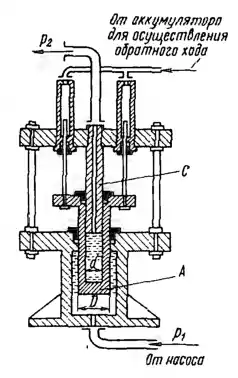
Рисунок 1.17
Гидравлический мультипликатор (повыситель давления) получает от насоса воду под давлением p1 = 0,5 МПа. Заполненный водой подвижный цилиндр А с внешним диаметром D = 200 мм скользит по неподвижной скалке С, имеющей диаметр d = 50 мм, создавая на выходе из повысителя давление p3. Определить давление р2, принимая силу трения в сальниках равной 10% от силы, развиваемой на цилиндре давлением F1, и пренебрегая давлением в линии обратного хода. Масса подвижных частей
мультипликатора m = 204 кг.
Задача 1.18
Цена - 80 руб. (pdf) - 100 руб. (word)
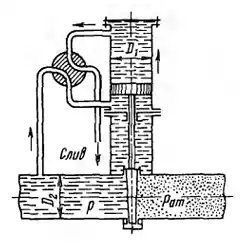
Рисунок 1.18
Определить диаметр D1 гидравлического цилиндра, необходимый для подъема задвижки, установленной на трубопроводе с избыточным давлением P = 1 МПа, если диаметр задвижки D2 = 1 м и масса подвижных частей устройства m = 204 кг. При расчете коэффициент трения задвижки в направляющих поверхностях принять равным f = 0,3, силу трения в цилиндре считать равной 5% от веса подвижных частей. Давление за задвижкой равно атмосферному.
Задача 1.19
Цена - 80 руб. (pdf) - 100 руб. (word)
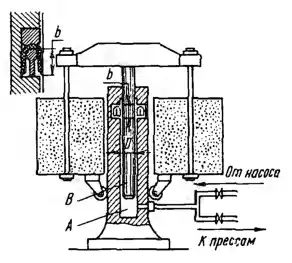
Рисунок 1.19
При зарядке гидравлического аккумулятора насос подает воду в цилиндр А, поднимая плунжер В вместе с грузом вверх. При разрядке аккумулятора плунжер, скользя вниз, выдавливает своим весом воду из цилиндра в гидравлические прессы.
Определить: 1. Давление воды при зарядке (развиваемое насосом) рз и при разрядке (получаемое прессами) аккумулятора, если масса плунжера вместе с грузом m = 104 т и диаметр плунжера D = 400 мм.
Плунжер уплотнен манжетой, высота которой b = 40 мм и коэффициент трения о плунжер f = 0,1.
2. Вычислить работу, затраченную на зарядку аккумулятора и работу, совершаемую аккумулятором при его разрядке, если полная высота подъема плунжера Н = 2 м.
3. Определить коэффициент полезного действия аккумулятора. Указание. Давление р воды в цилиндре аккумулятора считать одинаковым во всех точках. Величину Т силы трения манжеты о плунжер подсчитывать как произведение прижимающей силы на коэффициент трения: Т = рπDbf
Задача 1.20
Цена - 80 руб. (pdf) - 100 руб. (word)
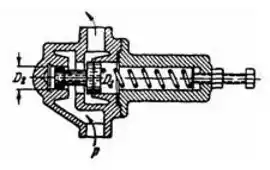
Рисунок 1.20
Определить предварительное поджатие х пружины, нагружающей дифференциальный предохранительный клапан, необходимое для того, чтобы клапан открывался при давлении P = 3 МПа. Диаметры поршней: D1 = 22 мм; D2 = 20 мм, а жесткость пружины С = 8 Н/мм.
Задача 1.21
Цена - 80 руб. (pdf) - 100 руб. (word)
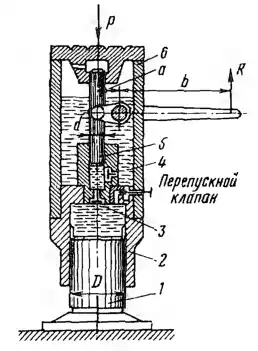
Рисунок 1.21
Гидравлический домкрат состоит из неподвижного поршня 1 и скользящего по нему цилиндра 2, на котором смонтированы корпус 3 (образующий масляную ванну домкрата) и плунжерный насос 5 ручного привода со всасывающим 4 и нагнетательным 3 клапанами. Определить рабочее усилие R на рукоятке приводного рычага насоса, необходимое для поднятия груза массой 12250 кг (Р = 120 кН), если диаметр поршня домкрата D = 200 мм, диаметр плунжера насоса d = 20 мм и плечи приводного рычага а = 60 мм и b = 700 мм. Принять к. п. д. насоса 0,65 и к. п. д. цилиндра 0,9.
Задача 1.26
Цена - 80 руб. (pdf) - 100 руб. (word)
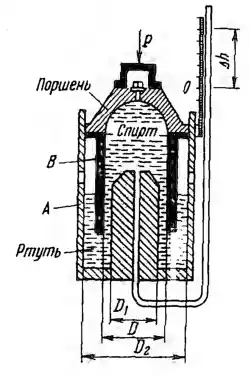
Рисунок 1.26
Для измерения малых сил используется жидкостный динамометр, состоящий из цилиндра А, наполненного до некоторого уровня ртутью, и погруженного в ртуть тонкостенного поршня В. Пространство под поршнем заполнено спиртом (δ = 0,8) и соединено со стеклянной трубкой пьезометра.
Нагружение поршня силой Р сопровождается увеличением давления под ним и подъемом уровня спирта в пьезометре, характеризующим величину измеряемой силы. Определить силу Р, если под ее действием уровень в пьезометре поднялся на высоту Δh = 0,25 м от начального положения 0. Диаметр поршня D = 0,2 м, диаметры цилиндра D1 = 0,1 м, и D2 = 0,21 м. Трением поршня о стенки цилиндра и влиянием подъема уровня спирта в пьезометре на объем спирта под поршнем пренебречь.
ГЛАВА 2.
СИЛЫ ДАВЛЕНИЯ ПОКОЯЩЕЙСЯ ЖИДКОСТИ НА ПЛОСКИЕ СТЕНКИ
Задача 1.4
Цена - 80 руб. (pdf) - 100 руб. (word)
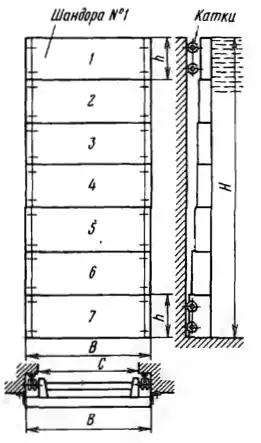
Рисунок 2.1
В плотине сделан прямоугольный проем размером НхС, через который вода поступает к турбине. При ремонте турбины этот проем закладывается семью специальными балками − шандорами. Размер каждой шандоры h х B = 1,2 х 3,4 м2. Все шандоры имеют по две пары катков.
1. Определить силы давления воды P1 и P7 на первую и седьмую шандоры и величины максимальных изгибающих моментов М1 и М7, для этих шандор, считая катки расположенными на концах шандор, а шандоры – свободно опертыми.
2. Найти расстояния Δh1 и Δh7, между центром давления и центром тяжести смоченной поверхности первой и седьмой шандор.
Задача 1.22
Цена - 80 руб. (pdf) - 100 руб. (word)
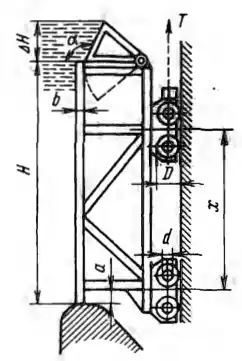
Рисунок 2.2
Затвор плотины высотой H = 6 м и шириной B = 30 м имеет поворотный сегментный клапан, который может увеличивать высоту подпора воды еще на ΔH = 1,5 м. Определить:
1. Горизонтальную силу давления воды на обшивку затвора при опущенном (P1) и поднятом (Р2) клапане. 2. Расстояние х между катковыми тележками, при котором нагрузки на тележки будут одинаковыми, когда сегментный клапан опущен (размер а = 0,2м). 3. Какое необходимо усилие, чтобы стронуть затвор с поднятым клапаном? Собственный вес затвора m = 150 т; внешний диаметр катков D = 0,6 м;
коэффициент трения качения k = 0,01 см; диаметр цапф d = 0,3 м; коэффициент трения скольжения в цапфах f = 0,15; b = 0,1 м; угол α = 120°.
Задача 2.3
Цена - 80 руб. (pdf) - 100 руб. (word)
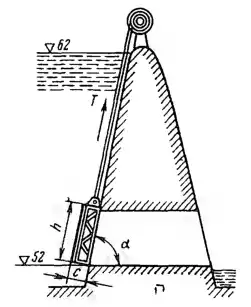
Рисунок 2.3
Плоский затвор, закрывающий выпускное отверстие в плотине, может перемещаться по ее стенке, наклоненной к горизонту под углом α = 70°. Размеры затвора: высота h =1,8 м; ширина b = 2,4 м; толщина с = 0,4 м; масса затвора m = 2 т. Определить: силу Т, необходимую для смещения закрытого затвора вверх, если коэффициент трения f = 0,35.
Задача 2.4
Цена - 80 руб. (pdf) - 100 руб. (word)
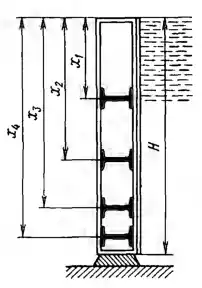
Рисунок 2.4
Сила давления воды через обшивку прямоугольного щита высотой H = 4 м и шириной В = 6 м передается на четыре горизонтальные балки. На каких расстояниях х от свободной поверхности следует их расположить, чтобы они были нагружены одинаково? Найти силу давления воды Р на весь щит и максимальный изгибающий момент М на балках, считая их свободно опертыми на концах.
Задача 2.5
Цена - 80 руб. (pdf) - 100 руб. (word)
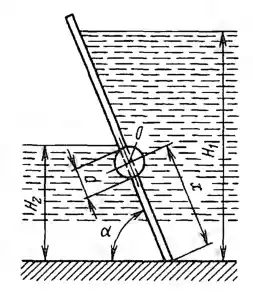
Рисунок 2.5
Щитовой затвор должен автоматически опрокидываться для пропуска воды при уровне последней Н1 > 6 м. Щит поворачивается на цапфах О диаметром d = 0,4 м, имеющих коэффициент трения f = 0,2. Ширина щита B = 8 м, его угол наклона α = 60°. Найти, на каком расстоянии х должна быть расположена ось поворота щита, если под щитом имеется постоянный уровень воды H2 = 3 м, и определить силу Р, воспринимаемую его опорами в момент опрокидывания.
Задача 2.6
Цена - 80 руб. (pdf) - 100 руб. (word)
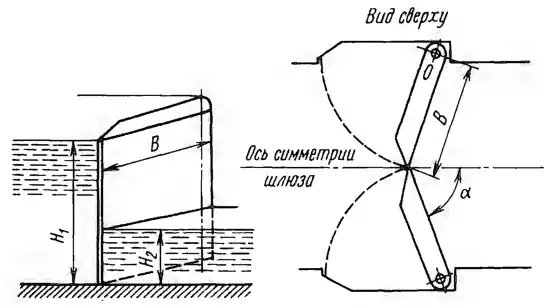
Рисунок 2.6
Двустворчатые ворота отгораживают шлюзовую камеру от канала с низовой стороны шлюза. При заполненном шлюзе вода по обе стороны ворот находится на уровнях H1 = 18 м и H2 = 6 м. Найти равнодействующую Р сил давления воды на каждую из створок ворот. На какой высоте х от дна проходит линия действия силы Р? Начертить эпюру нагрузки от воздействия воды на поверхность ворот. Определить силу Р0, воспринимаемую опорами, расположенными на оси вращения каждой из створок. При решении поверхность створки ворот считать плоской, шириной В = 16 м; угол α = 20°.
Задача 2.7
Цена - 80 руб. (pdf) - 100 руб. (word)
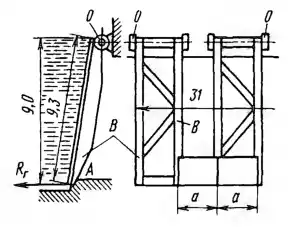
Рисунок 2.7
Стоечно - плоский затвор размером 9,3 х 31 м2 состоит из попарно соединенных стоек В, вращающихся вокруг оси О. Пространство между стойками при опущенном их положении закрывается набором плоских щитов шириной а = 1,8 м; для пропуска воды необходимое количество щитов поднимается вверх по стойкам. Определить для случая, когда вся поверхность затвора закрыта щитами:
1) Полную силу Р давления воды на затвор. 2) Горизонтальную составляющую Rг реакции порога А. 3) Наибольший изгибающий момент М стоек В (за исключением крайних).
Задача 2.8
Цена - 80 руб. (pdf) - 100 руб. (word)
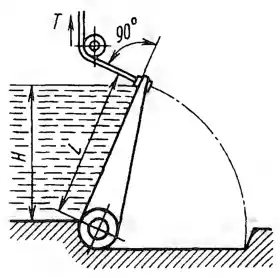
Рисунок 2.8
Клапанный затвор, имеющий плоскую поверхность размером L х В = 2,5 х 10 м создает подпор воды Н = 2,3 м. Определить:
1) Суммарную силу натяжения тросов Т, удерживающих затвор в заданном положении.
2) Наибольший изгибающий момент М на затворе.
3) Силу RA, воспринимаемую цапфами А.
Задача 2.9
Цена - 80 руб. (pdf) - 100 руб. (word)
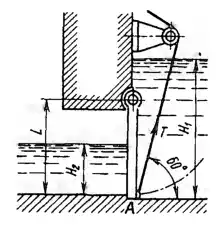
Рисунок 2.9
Прямоугольный поворотный щит размером L х B = 3 х 4 м закрывает выпускное отверстие плотины. Справа от щита уровень воды H1 = 5м, а слева H2 = 2 м. Определить:
1. Начальную силу Т натяжения тросов, необходимую для открытия щита.
2. С какой силой PA щит прижимается к порогу А в закрытом положении, если принять, что по боковым сторонам щита опоры отсутствуют?
Задача 2.10
Цена - 80 руб. (pdf) - 100 руб. (word)
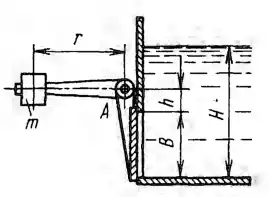
Рисунок 2.10
Квадратное отверстие размером В х В = 1 х 1 м в вертикальной стенке резервуара закрыто плоским поворотным щитом, который прижимается к стенке под действием груза массой m, расположенном на плече r = 1,5 м.
1. Найти минимальную массу груза m, достаточную для удержания воды в резервуаре на уровне H = 2 м, если расстояние от верхней кромки отверстия до оси вращения h = 0,3 м. Определить при этом реакции R цапф A щита.
2. Определить, какой наименьший вакуум pв над водой в резервуаре будет удерживать щит без груза?
Задача 2.11
Цена - 80 руб. (pdf) - 100 руб. (word)
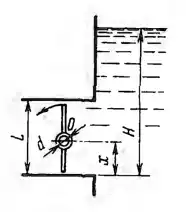
Рисунок 2.11
Прямоугольный поворотный затвор размером L х B = 2 х З м2 перекрывает выход воды из резервуара, уровень в котором равен H = 4 м. Определить:
1) На каком расстоянии х от нижней кромки затвора следует расположить его ось поворота, чтобы для открытия затвора нужно было преодолевать только момент трения в цапфах О. 2) Величину момента трения Мтр, если диаметр цапф d = 150 мм, а коэффициент трения f = 0,2.
Задача 2.12
Цена - 80 руб. (pdf) - 100 руб. (word)
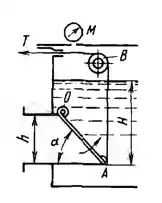
Рисунок 2.12
Поворотный клапан АО закрывает выход из бензохранилища в трубу квадратного сечения со стороной h = 0,3 м. Прямоугольная пластина клапана опирается на срез трубы, сделанный под углом α = 45 °. Определить (без учета трения) силу Т натяжения троса, необходимую для открытия клапана, если уровень бензина H = 0,85 м, а давление паров бензина равно по манометру М = 5 кПа. Плотность бензина ρ = 700 кг/м3.
Задача 2.13
Цена - 80 руб. (pdf) - 100 руб. (word)
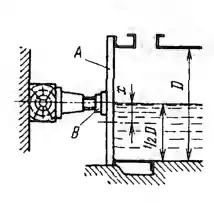
Рисунок 2.13
Заглушка А прижата к торцу горизонтального цилиндрического резервуара (диаметром D = 1,2 м) при помощи домкрата В, установленного в ее центре. Резервуар наполовину заполнен водой. Определить:
1) Наименьшую силу Р нажатия домкрата, необходимую для удержания заглушки.
2) Положение домкрата х, при котором необходимая сила нажатия будет минимальной, а также величину этой силы (Рх).
3) При каком вакууме V над водой в резервуаре заглушка могла бы удержаться без домкрата.
Задача 2.15
Цена - 80 руб. (pdf) - 100 руб. (word)
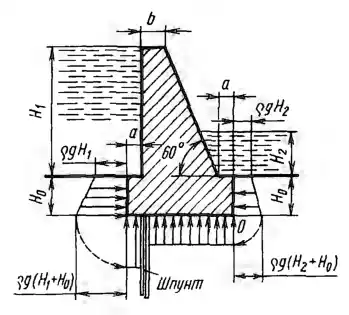
Рисунок 2.15
Бетонная плотина имеет следующие размеры: Н1 = 12 м, H0 = 3 м, а = 1 м, b = 2 м; уровень воды с низовой стороны H2 = 3 м. Так как грунт под плотиной водопроницаем, в него для предотвращения перетока воды забит шпунт. Проверить устойчивость плотины, найдя суммарный опрокидывающий М0 и восстанавливающий Мв моменты относительно точки О с учетом давления воды на подгрунтовую часть плотины (см. эпюру на эскизе). Все расчеты проводить на единицу длины плотины. Восстанавливающий момент от силы веса плотины в расчете на 1 м ее длины равен М = 13250 кН∙м/м.
Задача 2.16
Цена - 80 руб. (pdf) - 100 руб. (word)
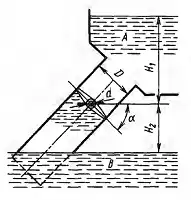
Рисунок 2.16
Дисковый затвор диаметром D = 1 м, установленный в трубе под углом α = 45° к горизонту, закрывает выход воды из резервуара А в резервуар В. Определить величину внешнего начального момента М, необходимого для открытия затвора против часовой стрелки, с учетом момента трения в цапфах затвора диаметром d = 0,15 м, если коэффициент трения f = 0,2. Задачу решить для двух случаев: 1) в трубе за затвором воздух под атмосферным давлением; 2) труба за затвором заполнена водой. Высоты уровней: H1 = 1,2 м и Н2 = 2 м.
Задача 2.17
Цена - 80 руб. (pdf) - 100 руб. (word)
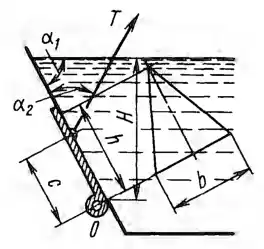
Рисунок 2.17
Определить минимально необходимое натяжение каната и силу реакции R0 на оси поворота О щита, закрывающего треугольное отверстие в плоской стенке, если заданы линейные размеры H = 3 м, h = 2 м; b = 1,6 м; с = 1,8 м и углы α1 = α2 = 60°.
Задача 2.18
Цена - 80 руб. (pdf) - 100 руб. (word)
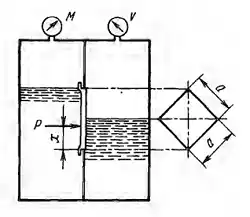
Рисунок 2.18
Замкнутый резервуар с нефтью (ρ = 920 кг/м3) разделен на две части плоской перегородкой, имеющей квадратное отверстие со стороной а = 1 м. Давление над нефтью в левой части резервуара определяется показанием манометра M = 15 кПа, а в правой - показанием вакуумметра V = 10 кПа. Уровни нефти указаны на эскизе. Найти величину Р и плечо х результирующей силы давления на крышку, закрывающую отверстие в перегородке.
Задача 2.19
Цена - 80 руб. (pdf) - 100 руб. (word)
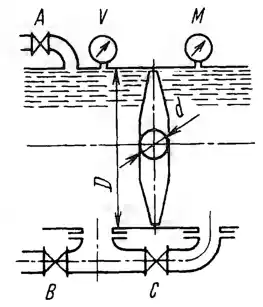
Рисунок 2.19
На трубопроводе установлен дисковый затвор диаметром D = 5,3 м с горизонтальной осью поворота и цапфами диаметром d = 0,65 м. При закрытии затвора трубопровод за ним остается заполненным водой, и тогда за затвором образуется вакуум, измеряемый вакуумметром V. Перед затвором давление измеряется манометром М, установленным (так же, как и вакуумметр) в верхней точке трубопровода. Трубопровод за затвором можно опорожнить открытием вентиля В при одновременном впуске воздуха через трубу А и закрытом вентиле С, тогда вакуум V за затвором будет равен нулю. Считать боковую поверхность диска затвора плоской.
1. Определить гидравлический момент M1, стремящийся открыть затвор при опорожненном трубопроводе за затвором и внешний начальный момент М2 для поворота затвора против часовой стрелки при показании манометра М = 600 кПа, если коэффициент трения в цапфах f = 0,15.
2. Найти начальный момент М3, необходимый для поворота затвора при заполненном трубопроводе за ним и показаниях манометра М = 600 кПа и вакуумметра V = 50 кПа.
Считать боковую поверхность диска затвора плоской.
Задача 2.20
Цена - 80 руб. (pdf) - 100 руб. (word)
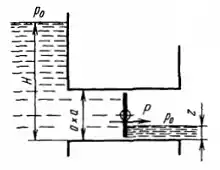
Рисунок 2.20
Слева от квадратного дроссельного затвора размером ахa уровень воды постоянен (H), а справа изменяется (z). Выразить в зависимости от z суммарную гидравлическую лу Р, действующую на затвор, и ее момент M относительно оси вращения затвора, проходящей через его центр тяжести. Указать наибольшие значения Р и М в интервале 0 ≤ z ≤ Н.
Задача 2.21
Цена - 80 руб. (pdf) - 100 руб. (word)
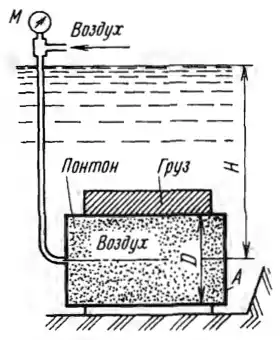
Рисунок 2.21
Цилиндрический понтон диаметром D = 1 м, погруженный под затонувший груз (плотность воды ρ = 1020 кг/м3), заполнен воздухом, давление которого по манометру М = 110 кПа. Определить силу давления Р на крышку А понтона и расстояние Δh от центра давления до центра тяжести крышки, если H = 10,5 м.
Задача 2.24
Цена - 80 руб. (pdf) - 100 руб. (word)
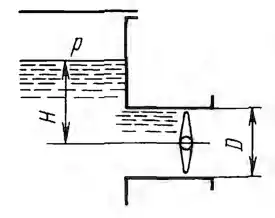
Рисунок 2.24
Закрытый резервуар с жидкостью (плотностью ρ = 900 кг/м3) имеет выпускную трубу диаметром D = 0,5 м, перекрытую дисковым затвором. Избыточное давление в резервуаре P = 8 кПа; H = 0,65 м. Найти силу давления Р на клапан затвора и момент М этой силы относительно оси поворота затвора. Каковы будут сила давления Р' и момент M', если над жидкостью давление станет равным атмосферному?
Исходные данные: ρ = 900 кг/м3; Н = 0,65 м; D = 0,5 м; P = 8 кПа
Задача 2.25
Цена - 80 руб. (pdf) - 100 руб. (word)
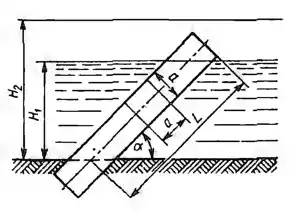
Рисунок 2.25
Определить результирующее воздействие давления воды на брус квадратного сечения со стороной а = 0,4 м, выступающий из непроницаемого грунта над поверхностью воды; глубина дна Н1 = 5 м, угол наклона бруса α = 45 °, Найти равнодействующую Р сил давления на этот же брус длиной L = 8 м при глубине дна Н2 = 6 м (весь брус под водой).
Исходные данные: а = 0,4 м; Н1 = 5 м; α = 45°; L = 8 м; Н2 = 6 м.
ГЛАВА 3.
СИЛЫ ДАВЛЕНИЯ ПОКОЯЩЕЙСЯ ЖИДКОСТИ НА КРИВОЛИНЕЙНЫЕ СТЕНКИ. ПЛАВАНИЕ ТЕЛ.
Задача 3.1
Цена - 80 руб. (pdf) - 100 руб. (word)
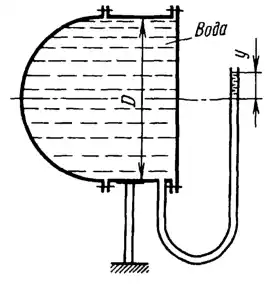
Рисунок 3.1
Определить величины и направления сил давления воды на плоское и полусферическое днища цилиндрическою сосуда диаметром D = 1 м в трех случаях: y = + D/5, y = − D/5, y = 0.
Показать на чертеже горизонтальные и вертикальные составляющие и полные силы давления воды на днища.
Задача 3.2
Цена - 80 руб. (pdf) - 100 руб. (word)
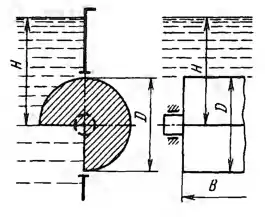
Рисунок 3.2
В прямоугольном окне вертикальной стенки резервуара установлен на цапфах цилиндрический затвор диаметром D = 0,8 м и длиной В = 3 м. Определить:
1) Усилие на цапфы и момент от воздействия воды на затвор в изображенном на эскизе положении при напоре Н = 1 м.
2) Каковы будут усилие на цапфы и момент, если повернуть затвор на 180.
Задача 3.3
Цена - 80 руб. (pdf) - 100 руб. (word)
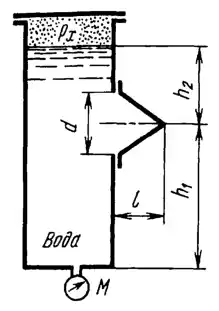
Рисунок 3.3
Показание манометра, присоединенного к днищу бака, равно M = 10 кПа. Найти давление рх воздуха, находящегося над водой, если h1 = 1,8 м и h2 = 1 м. Определить растягивающее Рраст и срезающее Рсрез усилия болтов, крепящих к вертикальной стенке бака коническую крышку с размерами d = 0,8 м и l = 0,6 м; массой крышки пренебречь. Найти зависимости этих сил от давления М.
Задача 3.4
Цена - 80 руб. (pdf) - 100 руб. (word)
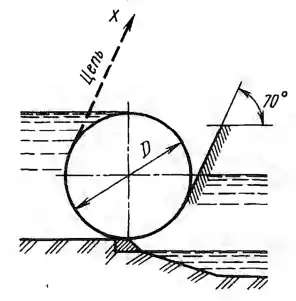
Рисунок 3.4
Цилиндрический затвор диаметром D = 1,2 м и длиной L = 16 м, масса которого 40 т, может открываться путем качения его вверх цепью по наклонным направляющим, составляющим угол α = 70° с горизонтом. Определить по величине и направлению силу давления воды на закрытый затвор. Найти натяжение цепи при трогании затвора с места и при выходе его из воды. Как изменятся сила давления воды на затвор и натяжение цепи, если уровень воды за плотиной поднимется до оси затвора?
Задача 3.5
Цена - 80 руб. (pdf) - 100 руб. (word)
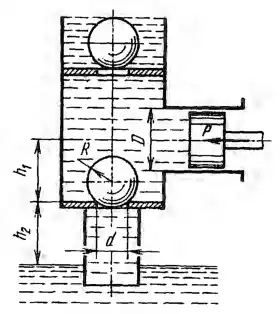
Рисунок 3.5
Определить силу, прижимающую стальной (относительный вес δ= 8) шаровой всасывающий клапан радиусом R = 100 мм к седлу, имеющему диаметр d = 125 мм, если диаметр насосного цилиндра D = 350 мм, а усилие
по штоку P = 4000 Н. Седло клапана расположено ниже оси цилиндра на расстоянии h1 = 0,5 м и выше свободной поверхности резервуара с атмосферным давлением на расстоянии h2 = 6,5 м, причем труба под клапаном заполнена водой.
Задача 3.6
Цена - 80 руб. (pdf) - 100 руб. (word)
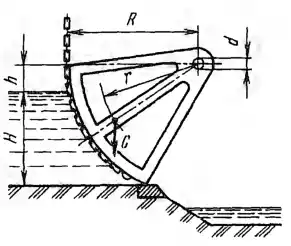
Рисунок 3.6
Секторный затвор радиусом R = 5 м и длиной L = 4,5 м поддерживает напор воды Н = 3,5 м. Для пропуска воды затвор поднимается цепью, поворачиваясь вокруг горизонтальной осина цапфах диаметром d = 150 мм. Вес затвора G = 3 т, его центр тяжести расположен на радиусе r = 0,75R. При закрытом затворе ось его вращения и верхний обрез сектора лежат в одной горизонтальной плоскости, расположенной выше свободной поверхности на расстоянии h = 1 м. Определить: 1. Силу, нагружающую подшипники закрытого затвора. 2. Силу, прижимающую затвор к порогу. 3. Начальное натяжение цепи при подъеме затвора (коэффициент трения в цапфах принять f = 0,3).
Задача 3.7
Цена - 80 руб. (pdf) - 100 руб. (word)
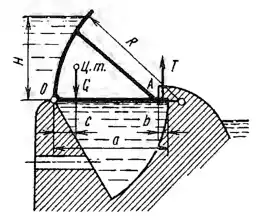
Рисунок 3.7
Секторный затвор плотины радиусом R = 4,5 м поддерживает напор воды Н = 3 м. Поворачиваясь вокруг оси 0, затвор может погружаться в выемку, сделанную в теле плотины и заполненную водой. Пренебрегая трением в опорах вращения, определить усилие Т, с которым затвор прижимается к уступу А плотины (приходящееся на 1 м, длины затвора), если вес 1 пог. м затвора 1 т, размеры а = 4 м и b = 0,3 м, плечо центра тяжести затвора с = 0,6 м.
Задача 3.8
Цена - 80 руб. (pdf) - 100 руб. (word)
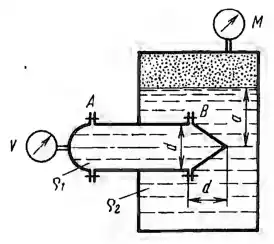
Рисунок 3.8
Горизонтальный цилиндрический сосуд диаметром d = 0,8 м с полусферической и конической тонкостенными крышками заполнен жидкостью плотностью ρ1. Правая половина цилиндра (с конической крышкой) вставлена в замкнутый резервуар и находится под уровнем другой жидкости плотностью ρ2 на глубине а = 2 м. Определить горизонтальные Рг и вертикальные Рв составляющие сил давления на полусферическую и коническую крышки А и В, если показание вакуумметра V = 10 кПа, показание манометра М = 30 кПа, ρ1 = ρ2 = 1000 кг/м3. Показать в виде векторов горизонтальные и вертикальные составляющие сил давления жидкости на полусферу и конус. Как изменятся силы при ρ1 = 0,8; ρ2 = 800 кг/м3.
Задача 3.9
Цена - 80 руб. (pdf) - 100 руб. (word)
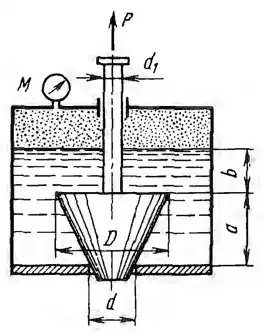
Рисунок 3.9
Отверстие в дне сосуда, содержащего масло (δ = 0,83), закрыто конической пробкой с размерами D = 100 мм, d = 50 мм и а = 100 мм, укрепленной на штоке d1 = 25 мм. Уровень масла расположен выше пробки на расстоянии b = 50 мм. Собственным весом пробки и трением в сальнике пренебречь. Определить: 1) Начальное усилие Р, необходимое для подъема пробки при показании манометра М = 10 кПа. 2) Давление воздуха в сосуде, при котором усилие Р окажется равным нулю.
Задача 3.10
Цена - 80 руб. (pdf) - 100 руб. (word)
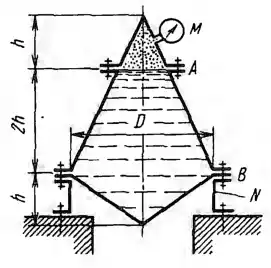
Рисунок 3.10
Определить усилия, нагружающие болтовые группы А и В сборного конического резервуара, содержащего воду, если h = 1 м, наибольший внутренний диаметр сосуда D = 3 м, а показание манометра М = 40 кПа.
Задача 3.11
Цена - 80 руб. (pdf) - 100 руб. (word)
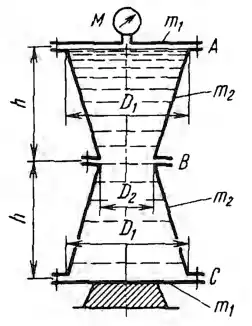
Рисунок 3.11
Определить усилия, нагружающие болтовые группы А, В и С симметричного сосуда размерами D1 = 1,8 м, D2 = 0,9 м и h = 1,2 м. m1 = 600 кг и m2 = 900 кг - веса крышки и конической обечайки сосуда. Сосуд заполнен водой, избыточное давление М = 50 кПа. Как изменятся усилия на болты, если вместо указанной на эскизе опоры подвесить сосуд за верхнюю крышку?
Задача 3.12
Цена - 80 руб. (pdf) - 100 руб. (word)
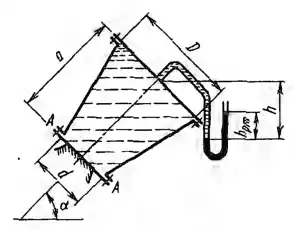
Рисунок 3.12
Определить растягивающие и срезающие усилия, нагружающие болты фланца А конического резервуара размерами D = 1 м; d = 0,5 м и а = 1 м, заполненного жидкостью плотностью ρ = 750 кг/м3. Давление в резервуаре измеряется ртутным манометром, показание которого hрт = 0,3 м и h = 0,5 м Угол наклона оси резервуара к горизонту α = 45° собственный вес резервуара не учитывать.
Задача 3.13
Цена - 80 руб. (pdf) - 100 руб. (word)
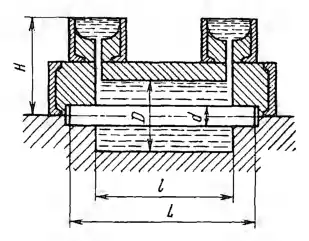
Рисунок 3.13
Для получения внутреннего отверстия в форму заложен цилиндрический стержень (относительная плотность δ = 2,5) диаметром d = 80 мм и длиной L = 1,2 м. Уровень чугуна в литнике расположен на высоте Н = 0,5 м над осью формы. Определить: 1) Максимальный изгибающий момент, действующий на стержень при заливке формы. 2) Вертикальную силу, которая стремится поднять, опоку при заливке формы. Стержень при отливке рассматривать как балку, свободно лежащую на двух опорах. Влиянием литников на искомую силу пренебречь.
Задача 3.15
Цена - 80 руб. (pdf) - 100 руб. (word)
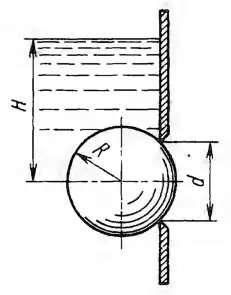
Рисунок 3.15
Каков наименьший уровень Н воды в сосуде, при котором стальной шар (δ = 8) радиусом R = 100 мм, перекрывающий круглое отверстие диаметром d = 1,5 R в вертикальной стенке, будет находиться в равновесии?
Задача 3.17
Цена - 80 руб. (pdf) - 100 руб. (word)
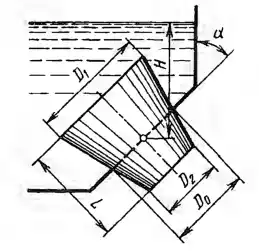
Рисунок 3.17
Отверстие диаметром D0 = 200 мм в плоской стенке, наклоненной к вертикали под углом α = 45°, перекрыто конической пробкой, размеры которой D1 = 300 мм, D2 = 150 мм и l = 300 мм. Уровень воды в сосуде Н = 500 мм. Определить силу давления воды на пробку.
Задача 3.19
Цена - 80 руб. (pdf) - 100 руб. (word)
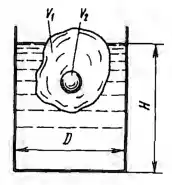
Рисунок 3.19
В цилиндрическом сосуде плавает кусок льда относительного веса δ1 = 0,9, в который впаян стальной шарик относительного веса δ2 = 7,8. Объем льда V1 = 12 дм3, объем шарика V2 = 50 см3.
1. Какая часть объема тела находится над водой?
2. Как изменится уровень Н в сосуде, когда лед растает, если диаметр сосуда D = 500 мм?
Ответить на поставленные вопросы еще для следующих двух вариантов задачи:
1. Вместо стального шарика объем V2 заполнен льдом.
2. Объем V2 представляет воздушную полость.
Задача 3.21
Цена - 80 руб. (pdf) - 100 руб. (word)
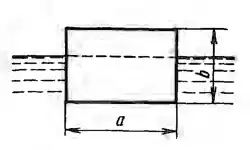
Рисунок 3.21
1. Прямоугольный параллелепипед относительной плотностью δ = 0,7 со стороной квадратного основания а = 250 мм и высотой b плавает в воде. Какому условию должна удовлетворять высота b, чтобы равновесие плавающего параллелепипеда было устойчивым?
2. В той же жидкости плавает куб со стороной а. Какому условию должен удовлетворять относительная плотность δ материала куба, чтобы равновесие плавающего куба было устойчивым?
Задача 3.23
Цена - 80 руб. (pdf) - 100 руб. (word)
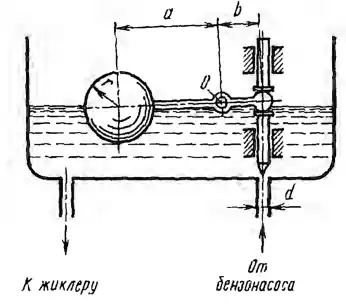
Рисунок 3.23
Бензин (δ = 0,7) под давлением р = 30 кПа подводится к поплавковой камере карбюратора по трубке диаметром d = 4 мм. Шаровой поплавок весом 25 г и игла (вес в бензине 12 г), перекрывающая доступ бензина, укреплены на рычаге (а = 40 мм, b = 15 мм), который может поворачиваться вокруг неподвижной оси О. Определить радиус r поплавка из условия, чтобы в момент открытия отверстия поплавок был погружен наполовину (трением в шарнирах и весом рычага пренебречь).
Задача 3.26
Цена - 80 руб. (pdf) - 100 руб. (word)
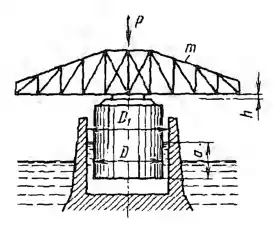
Рисунок 3.26
Поворотный пролет моста опирается на цилиндрический поплавок диаметром D = 3,4 м, плавающий в камере диаметром D1 = 3,6 м.
1) Определить погружение а поплавка в воду, если масса пролета с поплавком m = 30 т.
2) Осадку Н пролета при действии на него внешней силы Р = 100 кН.
Задача 3.35
Цена - 80 руб. (pdf) - 100 руб. (word)
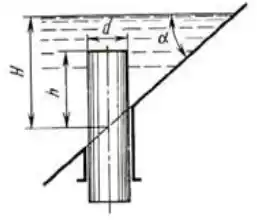
Рисунок 3.35
Определить горизонтальную Рг и вертикальную Рв силы давления воды на вертикальный цилиндр диаметром d = 400 мм, вставленный через отверстие в наклонной стенке (α = 45°) внутрь резервуара на высоту h = 1 м. Уровень воды H = 1,6 м.
Задача 3.36
Цена - 80 руб. (pdf) - 100 руб. (word)
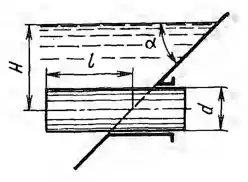
Рисунок 3.36
Определить горизонтальную Рг и вертикальную Рв силы давления воды на горизонтальный цилиндр диаметром d = 400 мм, который вставлен через отверстие в наклонной стенке (α = 45°) внутрь резервуара на расстояние l = 1000 мм. Уровень воды над осью цилиндра Н = 1 м.
ГЛАВА 4.
РАВНОВЕСИЕ ЖИДКОСТИ В ДВИЖУЩИХСЯ СОСУДАХ
Задача 4.1
Задача 4.1
Цена - 80 руб. (pdf) - 100 руб. (word)
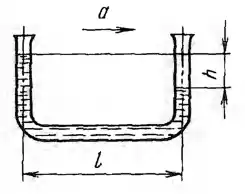
Рисунок 4.1
Для измерения ускорения горизонтально движущегося тела может быть использована закрепленная на нем U-образная трубка малого диаметра, наполненная жидкостью. С каким ускорением движется тело, если при движении установилась разность уровней жидкости в ветвях трубки, равная h = 5 см при расстоянии между ними l = 30 см?
Задача 4.7
Цена - 80 руб. (pdf) - 100 руб. (word)
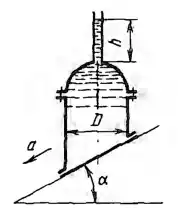
Рисунок 4.7
Определить горизонтальную и вертикальную силу давления на полусферическую крышку цилиндрического сосуда, D = 0,6 м, скользящего с ускорением скользящего с ускорением а = 5 м/сек2 по плоскости, наклоненной под углом а = 60° к горизонту, если сосуд заполнен водой до уровня h = 1 м в открытой трубке, присоединенной к верхней точке сосуда. Как изменятся эти силы, если сосуд остановить?
Задача 4.9
Цена - 80 руб. (pdf) - 100 руб. (word)
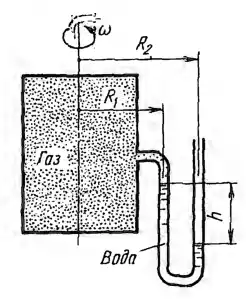
Рисунок 4.9
Найти зависимость показания h водяного манометра (радиусы ветвей R1 и R2 заданы), присоединенного к замкнутому сосуду, который наполнен газом, находящимся под вакуумом pв, от следующих параметров:
1) поступательного ускорения сосуда а, направленного по вертикали вверх и вниз;
2) угловой скорости ω сосуда.
Задача 4.13
Цена - 80 руб. (pdf) - 100 руб. (word)
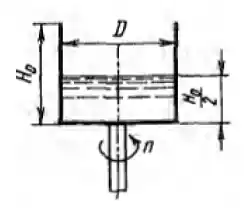
Рисунок 4.13
Найти частоту вращения n1 цилиндрического сосуда высотой H0 = 1,2 м и диаметром D = 0,8 м, наполненного жидкостью до высоты H0/2, при котором жидкость поднимается до краев сосуда. Определить частоту вращения n2 сосуда при которой в нем остается лишь половина первоначального объема жидкости.
Задача 4.15
Цена - 80 руб. (pdf) - 100 руб. (word)
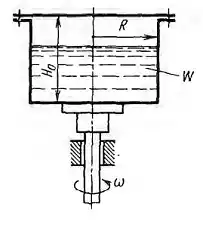
Рисунок 4.15
Замкнутый цилиндр размерами R = 0,4 м Н0 = 0,7 м содержит воду в объеме W = 0,25 м3 и вращается относительно вертикальной оси с угловой скоростью ω = 10 1/сек; 20 1/сек и 100 1/сек. Определить усилия, действующие при указанных оборотах на крышку цилиндра, если давление над водой равно атмосферному.
Задача 4.16
Цена - 80 руб. (pdf) - 100 руб. (word)
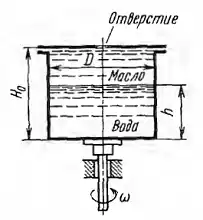
Рисунок 4.16
Цилиндрический сосуд диаметром D = 690 мм и высотой H0 = 500 мм заполнен водой до Н = 400 мм. Остальной объем сосуда заполнен маслом (δ = 0,8). Сосуд закрыт крышкой с малым отверстием в центре и приведен во вращение относительно центральной вертикальной оси. Определить, с какой угловой скоростью ω нужно вращать сосуд для того, чтобы поверхность раздела жидкостей коснулась дна сосуда. Найти усилия, действующие при этом на дно и крышку сосуда.
Задача 4.17
Цена - 80 руб. (pdf) - 100 руб. (word)
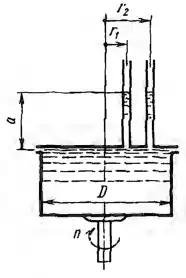
Рисунок 4.17
Цилиндрический сосуд диаметром D = 1,2 м, наполненный водой до высоты а = 0,6 м в пьезометрах одинакового диаметра, установленных на крышке сосуда на расстояниях r1 = 0,2 м и r2 = 0,4 м от оси, вращается с числом оборотов n = 60 об/мин. Определить силу давления на крышку сосуда и указать, как она будет меняться качественно, если поочередно выключать пьезометры.
ЧАСТЬ 2. ГИДРОДИНАМИКА
ГЛАВА 5.
ГИДРОДИНАМИЧЕСКОЕ ПОДОБИЕ. РЕЖИМЫ ДВИЖЕНИЯ ЖИДКОСТИ.
Задача 5.1
Цена - 100 руб. (pdf) - 120 руб. (word)
Сопротивление участка водопроводной трубы диаметром d = 50 мм с отводами и арматурой необходимо перед установкой проверить в лаборатории путем испытаний на воздухе.
1. Определить с какой скоростью υм следует вести продувку, сохраняя вязкостное подобие, если скорость воды в трубе будет равна υ = 2,5 м/сек.
2. Какова будет потеря напора hn при работе трубы на воде с указанной скоростью, если при испытании на воздухе потеря давления оказалась равной Δрм = 8,35 кПа.
Значения кинематического коэффициента вязкости (при t = 20℃) для воздуха νм = 0,156 Ст и воды ν = 0,01 Ст, плотность воздуха ρм = 1,166 кг/м3.
Задача 5.2
Цена - 100 руб. (pdf) - 120 руб. (word)
Требуется определить аэродинамическое сопротивление автомобиля (высотой h = 1,5 м) путем продувки его модели в аэродинамической трубе. Определить:
1) Каков должен быть размер модели hм для соблюдения подобия (равенство Rе), если максимальная скорость движения автомобиля равна v = 108 км/ч, а скорость продувки ограничена величиной vм = 45 м/с.
2) Какую силу лобового сопротивления Р будет испытывать автомобиль при максимальной скорости движения, если для модели при максимальной скорости продувки эта сила найдена равной Pм = 1500 Н. Вязкость и плотность воздуха принимать для натуры и модели одинаковыми.
Задача 5.3
Цена - 100 руб. (pdf) - 120 руб. (word)
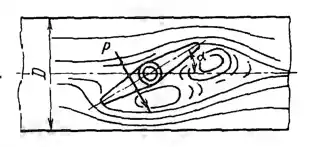
Рисунок 5.3
Для получения характеристик дискового затвора произведены испытания его модели диаметром Dм = 250 мм на воздухе. При расходе воздуха QМ = 1,6 м3/сек (плотность ρм =1,25 кг/м3) для определенного угла установки затвора α получены данные:
1) потеря напора в модели: ΔрМ = 2,7 кПа,
2) сила действия потока на затвор Pм = 140 Н;
3) момент этой силы относительно оси вращения затвора MМ = 3 Н∙м.
Предполагая, что испытания модели произведены в зоне турбулентной автомодельности, определить для затвора в натуре потерю напора hп, силу Р и момент М действия потока на затвор диаметром D = 2,5 м при расходе воды Q = 8 м3/с и том же угле установки.
Задача 5.4
Цена - 100 руб. (pdf) - 120 руб. (word)
При испытании на воде модели насадка, выходной диаметр которого dм = 30 мм, под статическим напором Hм = 50 м получены расход Qм = 18 л/с и средняя скорость в сжатом сечении струи υм = 30 м/с. Каков должен быть выходной диаметр d насадка в натуре и под каким напором Н он должен работать на воде, чтобы получить Q = 100 л/с и υ = 60 м/с. Считать, что испытания модели произведены в зоне турбулентной автомодельности, в силу чего коэффициенты истечения для модели и натуры одинаковы.
Задача 5.5
Цена - 100 руб. (pdf) - 120 руб. (word)
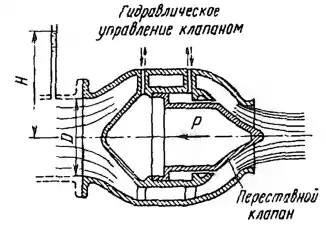
Рисунок 5.5
Игольчатый затвор, (в котором выходное отверстие перекрывается переставным клапаном обтекаемой формы) имеет в натуре входной диаметр D = 2 м и работает под статическим напором воды H = 100 м. При испытании на воде модели затвора, входной диаметр которой Dм = 0,2 м, под статическим напором Hм = 6 м получены расход Qм = 206 л/с и сила действия потока на полностью открытый клапан Pм = 600 Н. Определить:
1. Какой расход Q будет пропускать затвор в натуре. 2. Какая сила P будет действовать на клапан натурного затвора. Считать, что модель испытана в зоне турбулентной автомодельности.
Задача 5.6
Цена - 100 руб. (pdf) - 120 руб. (word)
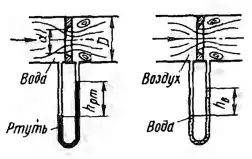
Рисунок 5.6
Диафрагма размерами d =100 мм и D = 200 мм, предназначенная для измерения расхода воздуха, тарируется путем испытания на воде. В результате испытаний получено, что минимальный расход воды, начиная с которого коэффициент расхода диафрагмы остается постоянным, равен Qмин = 16 л/с и при этом показание ртутного дифманометра, измеряющего перепад давлений на диафрагме, равно hрт = 45 мм. Определить: 1. Qмин при работе диафрагмы на воздухе. 2. Соответствующее этому расходу воздуха показание водяного дифманометра hв, присоединенного к диафрагме в тех же точках. Кинематический коэффициент вязкости воды ν = 10-6 м2/с, динамический коэффициент вязкости воздуха μ = 1,82∙10-4 П и его плотность ρ = 1,166 кг/м3. Указание. Значениям расхода Qмин при работе диафрагмы на различных жидкостях отвечает одинаковая величина числа Рейнольдса, представляющая границу зоны турбулентной автомодельности.
Задача 5.7
Цена - 100 руб. (pdf) - 120 руб. (word)
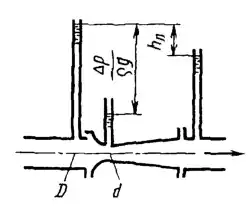
Рисунок 5.7
Труба Вентури с входным диаметром D = 300 мм и горловиной d = 150 мм, предназначенная для измерения расхода керосина тарируется путем испытания на воде ее модели, выполненной в масштабе 1:3 от натуры. Определить: 1. Каким должен быть расход воды Qм в модели для соблюдения подобия, если расход керосина в натурной трубе Q = 100 л/с; значения кинематической вязкости воды (t = 20 °C) νм = 0,01 Ст и керосина (t = 20 °C) ν = 0,045 Ст. 2. Каковы будут потеря напора hп и перепад давлений Δp в натурном расходомере, если при испытании модели на расходе, обеспечивающем соблюдение подобия, получено hп.м = 0,2 м и Δpм = 10 кПа. Плотность керосина ρ = 820 кг/м3.
Задача 5.8
Цена - 100 руб. (pdf) - 120 руб. (word)
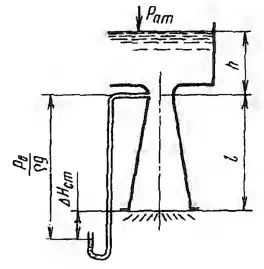
Рисунок 5.8
По вертикально расположенному диффузору длиной L = 500 мм вода должна вытекать в атмосферу из открытого резервуара, уровень в котором h = 0,5 м. Для предварительного определения пропускной способности диффузора производятся испытания его модели, выполненной в масштабе 1:2 от натуры. Закон моделирования выбран исходя из того, что поток в диффузоре является напорным, и его характер определяется только свойствами инертности и вязкости жидкости. Определить: 1) Каков должен быть при испытании модели на воде уровень hм в резервуаре опытной установки. 2) Какой расход Q будет пропускать диффузор в натуре, если при испытании модели получен расход QM = 30 л/с. 3) Какой вакуум рв будет во входном сечении натурного диффузора, если при испытании модели вакуум в этом сечении оказался равным рвм = 0,825 aт.
Задача 5.9
Цена - 100 руб. (pdf) - 120 руб. (word)
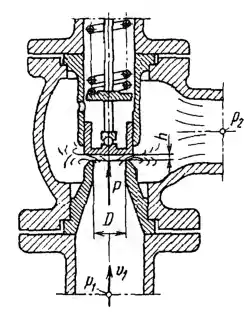
Рисунок 5.9
Предохранительный клапан диаметром Dм = 20 мм пропускает при открытии hм = 2 мм под перепадом давлений Δрм = р1− р2 = 0,5 МПа расход масла (ρм = 880 кг/м3 и νм = 2 Ст), равный QМ = 3 л/с. При этом сила давления, действующая на клапан, Pм = 80 Н. Определить: 1) Диаметр D клапана, пропускающего при соблюдении условий подобия (равенство относительных открытий h/D и чисел Rе) расход масла ρм = 880 кг/м3 и νм = 4 Ст), равный Q = 9 л/с. 2) Каков должен быть при этом перепад давлений ΔP и какова будет сила давления Р на клапан.
Задача 5.10
Цена - 100 руб. (pdf) - 120 руб. (word)
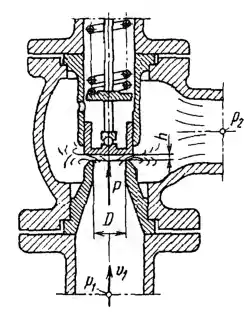
Рисунок 5.10
Предохранительный клапан диаметром Dм = 25 мм при открытии hм = 2 мм пропускает расход масла Qм = 5 л/с под перепадом давлений Δрм = р1 – р2 = 1 МПа. При этом сила давления на клапан Рн = 150 Н. Как следует изменить диаметр клапана, чтобы при увеличении расхода той же жидкости в 4 раза требуемый перепад давлений увеличился только в 2 раза? Найти открытие клапана h и действующую на него силу Р. Считать, что клапан работает в квадратичной зоне сопротивления.
Задача 5.11
Цена - 100 руб. (pdf) - 120 руб. (word)
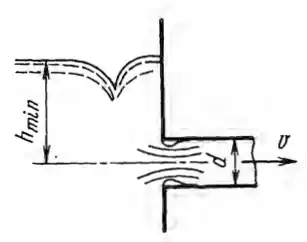
Рисунок 5.11
Путем модельных испытаний необходимо установить минимальное заглубление hмин всасывающей трубы насоса под уровнем нефти в резервуаре с тем, чтобы не возникало воронки и не происходило засасывания воздуха. Насос в натуре откачивает Q = 140 л/сек нефти ν = 0,75 Cт) по трубе диаметром d = 250 мм. Испытания производятся на геометрически подобной модели, линейный масштаб которой принят равным 1:5 от натуры. Так как условия входа нефти в трубу определяются в данном случае совместным влиянием свойств инертности, вязкости и весомости жидкости, при моделировании необходимо соблюдать равенство чисел Рейнольдса и Фруда. Определить: 1) Какова должна быть вязкость νм жидкости, используемой в модели. 2) Каков должен быть для модели откачиваемый расход Qм и какова будет при этом скорость vм в трубе. 3) При какой глубине hмин начнет образовываться воронка в натуре, если для модели испытания дали hмин м = 60 мм. В качестве модельной жидкости можно применять водный раствор глицерина, меняющий вязкость в зависимости от соотношения компонентов (при t = 20 °С) от ν = 0,01 Cт (вода) ν = 8 Cт (глицерин).
Задача 5.12
Цена - 100 руб. (pdf) - 120 руб. (word)
Рисунок 5.12
Истечение керосина (ν = 0,045 Ст) через отверстие диаметром d = 75 мм моделируется на воде (νм = 0,01 Ст) при соблюдении вязкостного и гравитационного подобия. Определить:
1) Диаметр отверстия dм для модели. 2) В каком отношении должны находиться высоты уровней для натуры h и модели hм? 3) В каком отношении при выполнении этих условий будут находиться расходы Q и Qм.
Задача 5.13
Цена - 100 руб. (pdf) - 120 руб. (word)
Рисунок 5.13
Истечение воды из под сегментного раствора изучается на модели, линейный масштаб которой относительно натуры принят 1:10. 1. Какой уровень Hм следует поддерживать перед затвором в модели, если в натуре H = 4 м. 2. Каковы будут расход Q и скорость v в сжатом сечении для затвора в натуре, если при испытании модели получены: Qм = 155 л/с и vм = 1,3 м/с. 3. Какова сила действия потока на затвор, если для модели она оказалась равной Рм = 55 Н. Моделирование осуществляется по критерию Фруда.
Задача 5.14
Цена - 100 руб. (pdf) - 120 руб. (word)
Водосливная плотина исследуется в лаборатории на геометрически подобной модели, выполненной в масштабе 1:20.
1. Определить напор hм на водосливе, который нужно принять для модели, если в натуре h = 3 м.
2. Найти расход через водосливное отверстие в натуре, если расход, полученный при испытании модели, равен Qм = 0,19 м3/сек.
3. Вычислить вакуум рв на гребне водослива в натуре, если на модели получен вакуум рвм = 2 кПа.
Ввиду незначительного влияния вязкости моделирование осуществляется по критерию Фруда.
Задача 5.15
Цена - 100 руб. (pdf) - 120 руб. (word)
Рисунок 5.15
В результате исследования на модели обтекания симметричного тела объемом Vм = 2 дм3, помещенного в вертикальный канал диаметром Dм = 200 мм, получено при скорости воды в канале vм = 10 м/с, что местная потеря напора на опытном участке канала равна hп.м = 5 м и сила, действующая на тело, Pм = 80 Н (направлена по потоку вниз). Считая, что испытания модели произведены в зоне турбулентной автомодельности, определить:1. Каковы будут потеря напора hп и сила P, действующая на геометрически подобное тело в натурном канале диаметром D = 500 мм при скорости v = 8 м/с? 2. При какой скорости v сила P будет равна нулю? 3. Какая сила будет действовать на тело при скорости v = 8 м/с, если натурный канал будет расположен горизонтально?
Задача 5.17
Цена - 100 руб. (pdf) - 120 руб. (word)
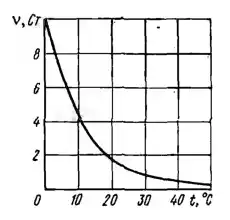
Рисунок 5.17
Машинное масло, для которого задана зависимость кинематического коэффициента вязкости ν от температуры, прокачивается по трубке диаметром d = 20 мм в количестве Q = 4 л/с. Определить режим движения при t = 10 °С и t = 40 °С и указать температуру, отвечающую критическому значению числа Рейнольдса (Rекр = 2300).
Задача 5.19
Цена - 100 руб. (pdf) - 120 руб. (word)
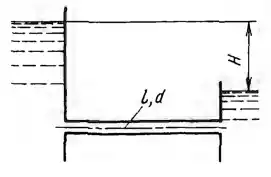
Рисунок 5.19
В трубопроводе диаметром d и длиной l под статическим напором Н движется жидкость с кинематическим коэффициентом вязкости ν. Получить выражение для критического напора, при котором происходит смена ламинарного режима турбулентным, учитывая в трубопроводе только потери на трение.
Задача 5.21
Цена - 100 руб. (pdf) - 120 руб. (word)
Для узкой кольцевой щели диаметром D = 250 мм и шириной b = 1 мм определить минимальный расход воды температурой 10 ℃ (ν = 0,013 Ст), при котором сохраняется турбулентный режим. Принять в качестве нижней границы этого режима Reкр = 3000. Будет ли влиять b на величину критического расхода (при сохранении условия, что b/D << 1)?
Задача 5.22
Цена - 80 руб. (pdf) - 100 руб. (word)
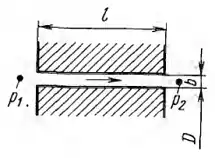
Рисунок 5.22
Для узкой кольцевой щели диаметром D = 250 мм и шириной b = 1 мм определить минимальный расход воды температурой 10 ℃ (ν = 0,013 Ст), при котором сохраняется турбулентный режим, принять в качестве нижней границы этого режима Reкр = 3000. Будет ли влиять b на значение критического расхода (при сохранении условия что b/D << 1)?
ГЛАВА 6.
ИСТЕЧЕНИЕ ЖИДКОСТИ ЧЕРЕЗ ОТВЕРСТИЯ. НАСАДКИ И ВОДОСЛИВЫ.
Задача 6.1
Цена - 100 руб. (pdf) - 120 руб. (word)
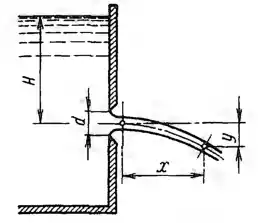
Рисунок 6.1
Определить коэффициенты расхода, скорости, сжатия и сопротивления при истечении воды в атмосферу через отверстие d = 10 мм под напором H = 2 м, если расход Q = 0,294 л/с, а координаты центра одного из сечений струи х = 3 м и у = 1,2 м.
Задача 6.2
Цена - 100 руб. (pdf) - 120 руб. (word)
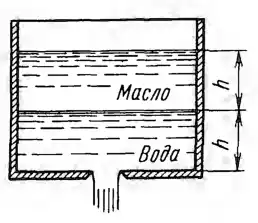
Рисунок 6.2
Определить, пренебрегая потерями, начальную скорость истечения жидкости из сосуда, заполненного слоями воды и масла (относительный вес δ = 0,8) одинаковой высоты h = 1 м. Сравнить полученный результат с начальной скоростью истечения при заполнении сосуда только водой или только маслом до уровня 2h.
Задача 6.3
Цена - 100 руб. (pdf) - 120 руб. (word)
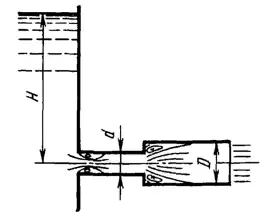
Рисунок 6.3
Для насадка, составленного из двух цилиндрических патрубков диаметрами d = 70 мм и D = 100 мм, определить коэффициенты сопротивления
и расхода. Найти предельный напор Нпр в случае истечения воды в атмосферу, принимая, что при H = Hпр вакуумметрическая высота в наименьшем сечении потока достигает 10 м. Построить график напоров.
Задача 6.4
Цена - 100 руб. (pdf) - 120 руб. (word)
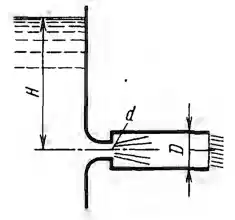
Рисунок 6.4
Для увеличения пропускной способности плавно сходящегося насадка, выходной диаметр которого d = 80 мм и коэффициент сопротивления ζ = 0,04, к нему присоединен цилиндрический патрубок. Определить диаметр патрубка, при котором пропускная способность полученного таким образом составного насадка будет наибольшей. Для этого же насадка определить в случае истечения воды предельный напор, при котором вакуум в узком сечении насадка достигнет 0,1 МПа. Построить график напоров.
Задача 6.5
Цена - 100 руб. (pdf) - 120 руб. (word)
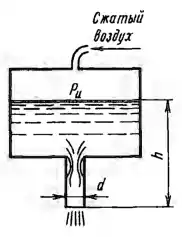
Рисунок 6.5
Определить до какого наибольшего избыточного давления ри сжатого воздуха над поверхностью бензина в баке истечение через цилиндрический насадок будет происходить с заполнением его выходного сечения. Каков будет при этом массовый расход бензина, если диаметр насадка d = 50 мм? Уровень бензина в баке h = 1,5 м. Плотность бензина ρ = 750 кг/м3, давление насыщенных паров равно рнп = 26,5 кПа. Атмосферное давление равно рат = 97 кПа. Принять коэффициент расхода насадка 𝜇 = 0,81 и коэффициент сжатия струи ε = 0,62
Задача 6.6
Цена - 100 руб. (pdf) - 120 руб. (word)
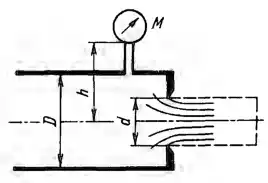
Рисунок 6.6
Определить расход воды через отверстие с острой кромкой диаметром d = 120 мм, выполненное в торце трубы диаметром D = 200 мм, если показание манометра перед отверстием M = 0,1 МПа и высота расположения манометра над осью трубы h = 1,5 м. Как изменится расход, если к отверстию присоединить цилиндрический насадок (пунктир)? Для насадка найти показание манометра, при котором произойдет срыв режима работы, принимая, что срыву соответствует абсолютное давление в сжатом сечении струи, равное нулю (атмосферное давление 0,1 МПа). Коэффициент сопротивления отверстия принять ζ = 0,04.
Задача 6.7
Цена - 100 руб. (pdf) - 120 руб. (word)
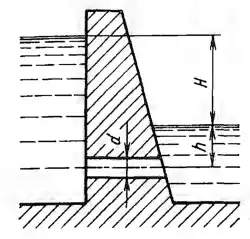
Рисунок 6.7
Через водоспуск плотины, имеющий форму цилиндрического насадка, необходимо пропускать расход Q = 2,3 м3/с при напоре Н = 10 м. Определить диаметр водоспуска d и минимальную глубину h затопления его оси под низовой уровень, необходимую, чтобы разрежение внутри насадка не превосходило 6 м вод. ст. Построить график напоров.
Задача 6.8
Цена - 100 руб. (pdf) - 120 руб. (word)
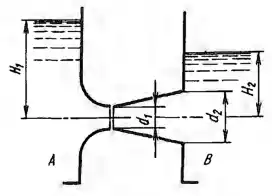
Рисунок 6.8
Вода перетекает из сосуда А в сосуд В через плавно сходящийся насадок с диаметром выходного сечения d1 = 100 мм и коэффициентом сопротивления ζ1 = 0,08 и приставленный к нему с небольшим зазором расходящийся конический насадок с выходным диаметром d2 = 150 мм и коэффициентом потерь φ2 = 0,3. При заданном уровне H1 = 2,5 м определить уровень H2, при котором протекающая по насадкам вода не будет выливаться через зазор, а атмосферный воздух не будет засасываться внутрь насадков. Построить график напоров. Указание. В сечении потока, соответствующем зазору между насадками, давление должно равняться атмосферному.
Задача 6.9
Цена - 100 руб. (pdf) - 120 руб. (word)
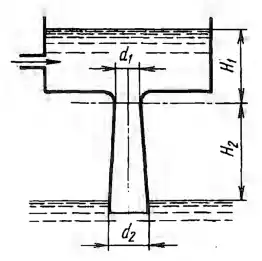
Рисунок 6.9
Вода перетекает из верхнего резервуара в нижний по диффузору, диаметры которого d1 = 100 мм и d2 = 150 мм. Коэффициент сопротивления входного участка ζвх = 0,06, а коэффициент потерь в диффузоре φд = 0,2. Определить, при каком уровне Н1 в верхнем резервуаре абсолютное давление в узком сечении диффузора станет равным нулю, если это сечение расположено над нижним уровнем на высоте H2 = 1,2 м. Атмосферное давление принять равным рат = 98 кПа.
Задача 6.10
Цена - 100 руб. (pdf) - 120 руб. (word)
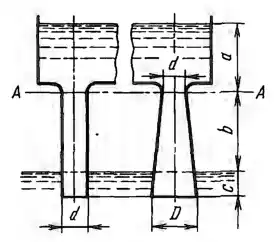
Рисунок 6.10
Сравнить расходы при перетекании воды из верхнего бака в нижний через цилиндрическую трубу диаметром d = 300 мм, и через диффузор с тем же диаметром входа и выходным диаметром D = 600 мм, если уровни в баках постоянны, а высоты равны: а = 0,8 м, b = 1,4 м, с = 0,6 м. Коэффициент сопротивления сходящегося входного участка ζc = 0,05, коэффициент потерь в диффузоре φ = 0,25 и коэффициент сопротивления трения в трубе λ = 0,025. В обоих случаях определить также давление в сечении А-А и построить пьезометрические линии, откладывая напоры по горизонтали от осевой линии (метод построения см. в гл. 9).
Задача 6.11
Цена - 100 руб. (pdf) - 120 руб. (word)
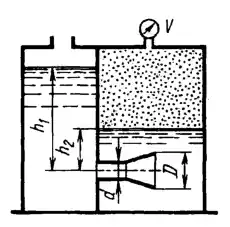
Рисунок 6.11
Бензин (δ = 0,75) перетекает из открытого левого бака в закрытый правый бак. Уровни в баках и вакуум в правом баке поддерживаются постоянными и равными h1 = 7 м, h2 = 3 м, V = 30 кПа. Определить расходы бензина через цилиндрический насадок диаметром d = 60 мм и через составной насадок, полученный путем добавления к цилиндрическому насадку конического диффузора с выходным диаметром D = 80 мм и коэффициентом потерь φд = 0,3. Для цилиндрического насадка принять коэффициент расхода 𝜇1 = 0,81 и коэффициент сжатия струи на входе в насадок ε = 0,62. Для обоих случаев определить наименьшее давление в сжатом сечении внутри насадка и построить пьезометрическую линию. Давление насыщенных паров бензина рнп = 15 кПа, атмосферное давление принять рат = 100 кПа.
Задача 6.12
Цена - 100 руб. (pdf) - 120 руб. (word)
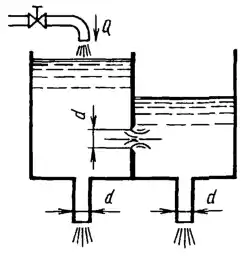
Рисунок 6.12
В бак, разделенный на две секции перегородкой, имеющей отверстие диаметром d = 100 мм, с острой кромкой, поступает вода в количестве Q = 80 л/с. Из каждой секции вода вытекает через цилиндрический насадок, диаметр которого равен диаметру отверстия в перегородке. Определить расход через каждый насадок при установившемся режиме, предполагая, что отверстие в перегородке является затопленным. Как надо изменить диаметр насадка в левой секции, чтобы расходы через оба насадка стали равными?
Задача 6.13
Цена - 100 руб. (pdf) - 120 руб. (word)
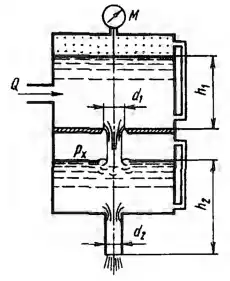
Рисунок 6.13
Вода из верхней секции замкнутого бака перетекает в нижнюю через отверстие d1 = 30 мм, а затем через цилиндрический насадок d2 = 20 мм вытекает в атмосферу. Определить расход через насадок, если при установившемся режиме показание манометра М = 50 кПа, а уровни в водомерных стеклах h1 = 2 м и h2 = 3 м. Найти при этом давление рх над уровнем воды в нижней секции бака. Построить эпюры давлений по оси сосуда.
Задача 6.15
Цена - 100 руб. (pdf) - 120 руб. (word)
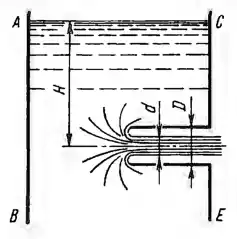
Рисунок 6.15
Определить коэффициент сжатия струи при истечении из большого бака через внутренний цилиндрический насадок с тонкой стенкой, диаметр D которого мал по сравнению с напором H. Пренебрегать потерями напора и считать, что по стенкам AB и CE, вследствие их удаленности от входа в насадок, давление распределяется по гидростатическому закону.
Задача 6.16
Цена - 100 руб. (pdf) - 120 руб. (word)

Рисунок 6.3
Определить расход и диаметр струи при истечении через малое отверстие диаметром D = 10 мм с острой кромкой под напором H = 1 м следующих жидкостей: воды (кинематический коэффициент вязкости ν = 10-2 Ст), легкой нефти (ν = 25,6∙10-2 Ст) и глицерина (ν = 860∙10-2 Ст). При решении воспользоваться зависимостью коэффициентов истечения от числа Рейнольдса, приведенной на рис. 6-3.
Задача 6.17
Цена - 100 руб. (pdf) - 120 руб. (word)
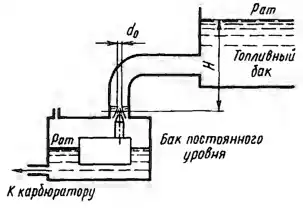
Рисунок 6.17
Бензин из топливного бака перетекает в находящийся перед карбюратором бачок постоянного уровня через диафрагму с отверстием d0 = 2 мм. Определить диаметр струи и расход бензина через отверстие при напоре H = 0,4 м и полностью открытом отверстии, пользуясь для определения коэффициентов истечения их зависимостью от Rе, приведенной на рис. 6.17.2. Кинематический коэффициент вязкости бензина ν = 0,93∙10-6 м2/с.
Задача 6.18
Цена - 100 руб. (pdf) - 120 руб. (word)
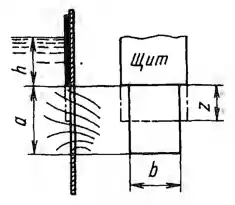
Рисунок 6.18
Вода вытекает через большое прямоугольное отверстие высотой а = 0,6 м, заглубленное под постоянный уровень на h = 0,4 м. Определить, какую часть z высоты отверстия надо перекрыть щитом, чтобы расход уменьшился в 2 раза. Коэффициент расхода при обоих положениях щита принимать одинаковым.
Задача 6.19
Цена - 100 руб. (pdf) - 120 руб. (word)
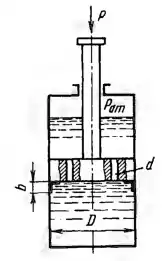
Рисунок 6.19
Определить скорость перемещения поршня гидротормоза диаметром D = 200 мм, нагруженного силой Р = 120 кН, если перетекание жидкости из нижней полости цилиндра в верхнюю происходит через два отверстия в поршне, диаметр которых d = 10 мм. Коэффициент расхода отверстий μ = 0,6, плотность жидкости ρ = 865 кг/м3. Коэффициент трения в манжете поршня шириной b = 25 мм равен f = 0,15.
Задача 6.21
Цена - 100 руб. (pdf) - 120 руб. (word)
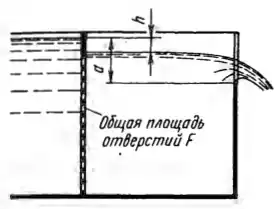
Рисунок 6.21
Вода вытекает из бака через прямоугольный водослив с тонкой стенкой, который используется как измеритель расхода. Перед водосливом установлена успокоительная решетка из перфорированного листа, общая площадь сверлении в котором F = 0,25 м2. Сверления можно рассматривать как независимо работающие отверстия с острой кромкой, истечение через которые происходит под уровень (μ = 0,6). Определить расход воды через водослив, если уровень перед успокоительной решеткой выше порога водослива на а = 400 мм. Ширина водослива b = 0,8 м (боковое сжатие отсутствует), его коэффициент расхода принять m = 0,42. Каков при этом перепад h на решетке?
Задача 6.26
Цена - 100 руб. (pdf) - 120 руб. (word)
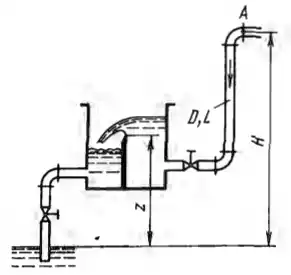
Рисунок 6.26
Для ограничения вакуума в сифонном трубопроводе на его нисходящей ветви установлен гидравлический затвор в виде прямоугольного водослива с тонкой стенкой. Диаметр трубопровода D = 200 мм, его верхняя точка А расположена выше уровня, под который сливается вода, на H = 10 м. Определить, на какой высоте z от нижнего уровня следует поместить порог водослива, чтобы при расходе Q = 80 л/с вакуум в точке А не превосходил 6 м. Длина участка трубопровода от точки А до затвора L = 12 м, коэффициент сопротивления открытой задвижки ζз = 0,15 и каждого из отводов ζо = 0,2. Коэффициент сопротивления трения в трубе принять λ = 0,02. Ширина порога водослива В = 500 мм, его коэффициент расхода принять m = 0,41.
ГЛАВА 7.
МЕСТНЫЕ СОПРОТИВЛЕНИЯ. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЯ РАСХОДА И СКОРОСТИ.
ЭЛЕМЕНТЫ СИСТЕМ ГИДРОАВТОМАТИКИ.
Задача 7.2
Цена - 100 руб. (pdf) - 120 руб. (word)
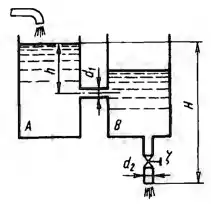
Рисунок 7.2
Из бака А, в котором поддерживается постоянный уровень, вода протекает по цилиндрическому насадку диаметром d1 = 20 мм в бак В, из которого сливается в атмосферу по короткой трубке диаметром d2 = 25 мм. Напор H = 900 мм, а ось патрубка размещена на глубине h = 400 мм под уровнем воды в баке А. Найти зависимость расхода воды, перетекающей из бака A в бак В, от коэффициента сопротивления ζ крана, установленного в трубке. Определить наименьшее значение ζ, начиная с которого дальнейшее увеличение открытия крана (т. е. уменьшение его ζ) не будет давать увеличения расхода. Потери на трение в трубке не учитывать.
Задача 7.4
Цена - 100 руб. (pdf) - 120 руб. (word)
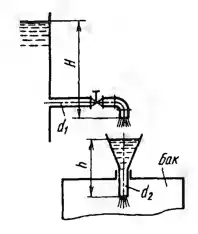
Рисунок 7.4
Заполнение бака бензином происходит через воронку диаметром d2 = 50 мм, высотой h = 400 мм с коэффициентом сопротивления ζ = 0,25. В воронку бензин заливается из резервуара с постоянным уровнем по короткой трубе диаметром d1 = 30 мм с краном и угольником, коэффициенты сопротивления которых соответственно равны ζк = 8,5 и ζу = 0,8. Определить, какой наибольший напор Н можно иметь в резервуаре, чтобы воронка не переполнялась, и каков при этом расход бензина, поступающего в бак. Потери на трение в трубе не учитывать.
Задача 7.5
Цена - 100 руб. (pdf) - 120 руб. (word)
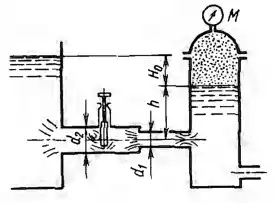
Рисунок 7.5
По короткому трубопроводу, участки которого имеют диаметры d1 = 70 мм и d2 = 100 мм, вода перетекает из закрытого бака с избыточным давлением воздуха на поверхности М = 195 кПа в открытый бак при постоянной разности уровней Н0 = 5 м. Ось трубопровода заглублена под уровень воды в правом баке на h = 2 м. Определить расход (пренебрегая потерями на трение) для случая, когда задвижка полностью открыта и ее коэффициент сопротивления ζ = 0, и для случая, когда задвижка открыта на 0,25 ее хода и ζ = 16. Для рассмотренных выше двух случаев построить линии напора и пьезометрические линии. При построении пьезометрической линии найти приближенно давление в сжатом сечении после задвижки, если при указанном ее неполном открытии проходная площадь задвижки составляетFс/F2 = 0,32 от площади трубы, а коэффициент сжатия высечении потока после задвижки ε = 0,65. Указание. При подсчете давления учитывать, что после сжатого сечения за задвижкой происходит потеря на внезапное расширение, определяемая формулой (7-2).
Задача 7.6
Цена - 100 руб. (pdf) - 120 руб. (word)
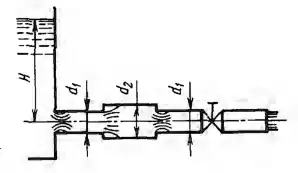
Рисунок 7.6
Вода вытекает в атмосферу по короткому горизонтальному трубопроводу, в котором установлен вентиль, под постоянным напором H = 16 м. Диаметры участков трубопровода равны d1 = 50 мм и d2 = 70 мм. Коэффициент сопротивления вентиля ζв = 4,0. Определить расход в трубе, учитывая только местные потери. Построить линию полного напора и пьезометрическую линию.
Задача 7.7
Цена - 100 руб. (pdf) - 120 руб. (word)
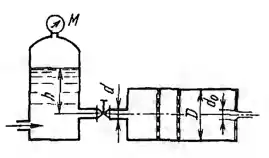
Рисунок 7.7
В экспериментальной установке изучается истечение воды через круглое отверстие с острой кромкой диаметром d0 = 50 мм, выполненное в торцовой стенке горизонтального бака диаметром D = 200 мм. Бак снабжен двумя успокоителями из перфорированного листа. Сверления в каждом листе имеют суммарную площадь, равную 1/5 площади сечения бака, и могут рассматриваться как независимо работающие отверстия с острой кромкой, истечение через которые происходит под уровень. Вода подается в бак из резервуара по короткой подводящей труба диаметром d = 50 мм, снабженной вентилем, коэффициент сопротивления которого ζв = 4,6. Определить скорость истечения и расход через отверстие при показании манометра на резервуаре М = 0,15 МПа и уровне h = 1 м, принимая для отверстия в баке и сверлений в сетках коэффициент сопротивления ζс = 0,06 и сжатия струи ε = 0,62. Построить графики напоров.
Задача 7.8
Цена - 100 руб. (pdf) - 120 руб. (word)
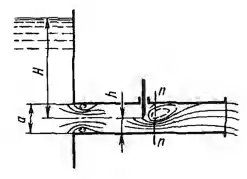
Рисунок 7.8
Вода вытекает в атмосферу по короткой трубе квадратного сечения со стороной a = 200 мм при постоянном напоре H = 10 м. Определить расход по трубе и вакуум в сжатом сечении n-n в зависимости от степени открытия задвижки h/a. Подсчеты провести для двух значений h/a, используя соответствующие им величины коэффициента сопротивления задвижки ζз и сжатия струи ε в сечении n-n: h/a = 0,8; ζз = 0,39; ε = 0,80 и h/a = 0,1; ζз = 193; ε = 0,67. Коэффициент сопротивления входа в трубу принять ζвх = 0,5, потери трения не учитывать. В обоих случаях построить графики напоров. Указание. При определении вакуума в сечении n-n считать, что расширение потока после этого сечения приводит к потере напора, определяемой формулой (7-2).
Задача 7.9
Цена - 100 руб. (pdf) - 120 руб. (word)
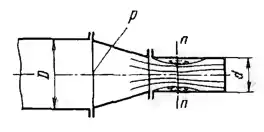
Рисунок 7.9
Трубопровод диаметром D = 160 мм оканчивается насадком, который состоит из конуса и короткого цилиндрического участка диаметром d = 80 мм. Коэффициент сопротивления конуса, отнесенный к скорости в сжатом сечении n-n, равен ζ = 0,1; коэффициент сжатия струи в этом сечении ε = 0,8. Пренебрегая упругостью паров воды, найти предельное давление р перед насадком, при котором он перестанет работать сплошным выходным сечением, т. е. при котором вакуум в сечении n-n насадка достигнет 10 м. При этом давлении найти расход через насадок и построить график напоров по его длине.
Задача 7.10
Цена - 100 руб. (pdf) - 120 руб. (word)
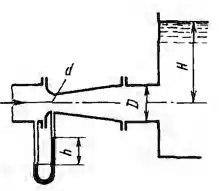
Рисунок 7.10
В трубопроводе диаметром D = 50 мм, подающем воду в бак с постоянным уровнем H = 1,5 м, установлена труба Вентури с горловиной диаметром d = 25 мм. Коэффициент сопротивления сходящегося участка расходомера ζр = 0,06, коэффициент потерь в его диффузоре φд = 0,20. Определить:
1) Какой наибольший расход можно подавать в бак до появления кавитации в расходомере, если упругость паров воды рнп = 19,6 кПа (t = 60°С). 2) Каково будет при этом расходе показание h ртутного дифференциального манометра.
Задача 7.11
Цена - 100 руб. (pdf) - 120 руб. (word)
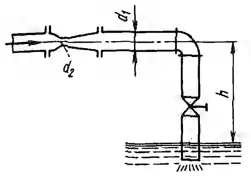
Рисунок 7.11
По трубопроводу диаметром d1 = 50 мм, в котором установлена труба Вентури с горловиной d2 = 25 мм, вода сливается под постоянный уровень, расположенный ниже оси расходомера на Н = 2 м. Коэффициент потерь в диффузоре расходомера φд = 0,25 и коэффициент сопротивления угольника ζуг = 1. Определить, пренебрегая потерями на трение:
1) Какой наибольший расход можно пропускать по трубопроводу при полностью открытом вентиле (ζв = 7), чтобы вакуум в горловине расходомера не превышал 6 м вод. ст. 2) Каким должен быть коэффициент сопротивления вентиля, чтобы при найденном выше расходе давление в горловине расходомера равнялось атмосферному.
Задача 7.12
Цена - 100 руб. (pdf) - 120 руб. (word)
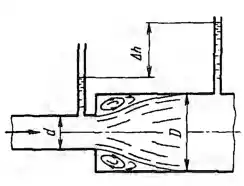
Рисунок 7.12
Определить отношение диаметров D/d, при котором в случае внезапного расширения трубы будет иметь место наибольшая разность показаний пьезометров dh для любого заданного расхода.
Задача 7.13
Цена - 100 руб. (pdf) - 120 руб. (word)
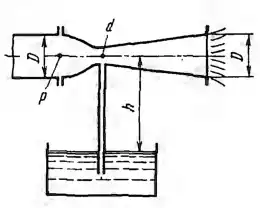
Рисунок 7.13
Труба диаметром D = 40 мм имеет на конце сходящийся насадок с горловиной d = 20 мм и коэффициентом сопротивления ζ = 0,08, переходящий в диффузор с коэффициентом потерь φд = 0,3, из которого вода вытекает в атмосферу. Какой расход надо пропускать по трубе и какое при этом будет давление р перед насадком, чтобы в горловину начала поступать вода, подсасываемая на высоту h = 2 м из открытого сосуда? Построить график напоров при этом расходе.
Задача 7.15
Цена - 100 руб. (pdf) - 120 руб. (word)
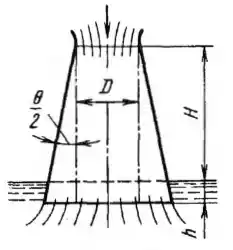
Рисунок 7.15
В отсасывающей трубе водяной турбины, выполненной в виде конического диффузора с входным диаметром D = 0,5 м и углом раскрытия θ = 16°, расход воды равен Q = 1,0 м3/с. Определить:
1. Вакуум во входном сечении, которое расположено над уровнем воды на высоте Н = 1,6 м, если выходное сечение трубы заглублено под уровень на h = 0,4 м, а коэффициент потерь в диффузоре φд = 0,3. 2. Каким станет вакуум во входном сечении, если диффузор заменить цилиндрической трубой диаметром D (штрих-пунктир) с коэффициентом сопротивления трения λ = 0,03. В обоих случаях построить пьезометрические линии по высоте трубы.
Задача 7.17
Цена - 100 руб. (pdf) - 120 руб. (word)
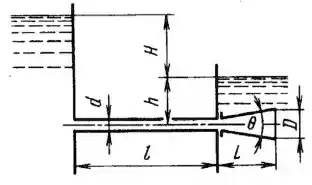
Рисунок 7.17
Для увеличения пропускной способности короткой трубы длиной l = 800 мм и диаметром d = 80 мм, работающей под постоянным напором H = 10 м, к ней присоединен конический диффузор с углом раскрытия Θ = 16° и коэффициентом потерь φд = 0,3. Определить выходной диаметр диффузора D и соответствующую ему длину L, при которых расход воды по трубе будет наибольшим. Во сколько раз присоединение такого диффузора увеличит расход по трубе? Коэффициент сопротивления трения в трубе принять λ = 0,03. Построить пьезометрическую линию для этой системы при заданном заглублении оси трубы под нижний уровень, равном h = 3 м. Указание. См. пример во введении гл. 6.
Задача 7.18
Цена - 100 руб. (pdf) - 120 руб. (word)
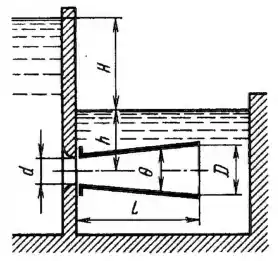
Рисунок 7.18
Вода перетекает из одного резервуара в другой под постоянным напором Н по горизонтальному коническому диффузору с диаметром входа d = 200 мм и длиной L = 1200 мм. Пренебрегая сопротивлением входа в диффузор, определить величину выходного диаметра D, при котором пропускная способность диффузора будет максимальной. Коэффициент потерь в диффузоре задан таблично в зависимости от угла раскрытия:
Таблица 1. Сопротивление диффузора при различных углах раскрытия.
|
θ, ° |
8 |
10 |
12 |
14 |
16 |
|
φд |
0,15 |
0,175 |
0,2 |
0,25 |
0,30 |
Определить также, при каком наибольшем напоре Н может работать такой диффузор, если он заглублен под уровень на h = 2 м, а вакуум в его входном сечении не должен превышать 8 м. Построить для этого случая график напоров.
Задача 7.35
Цена - 100 руб. (pdf) - 120 руб. (word)
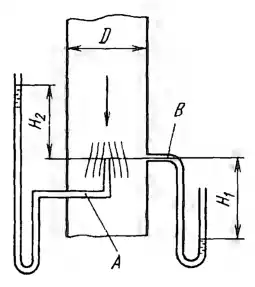
Рисунок 7.25
На оси вертикальной трубы диаметром D = 200 мм установлена трубка A для измерения полного напора. В этом же сечении установлена пьезометрическая трубка В, измеряющая статическое давление в сечении. Определить расход воды в трубе, если уровень воды в трубке А находится выше мерного сечения на H2 = 0,3 м, а уровень в трубке В - ниже мерного сечения на Н1 = 0,2 м. Отношение средней скорости в сечении к скорости на оси трубы принять равным 0,84.
Задача 7.36
Цена - 100 руб. (pdf) - 120 руб. (word)
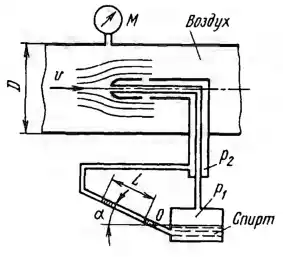
Рисунок 7.36
Скоростная трубка, установленная вдоль оси воздухопровода диаметром D = 200 мм, дает на спиртовом микроманометре с наклонной шкалой показание L = 75 мм. Плотность спирта в манометре ρс = 800 кг/м3, наклон трубки манометра к горизонту sinα = 0,2. Давление воздуха в мерном сечении равно по манометру М = 40 кПа, его температура t = 16 ℃. Барометрическое давление Pат = 98 кПа. Определить весовой расход воздуха, приняв коэффициент трубки равным единице (перепад давлений (P1−P2)/ρ∙g воздуха в ветвях трубки равен скоростному напору в мерной точке), а отношение средней скорости в трубе к измеряемой трубкой скорости на ее оси k = vcp/v = 0,84.
ГЛАВА 8.
ЛАМИНАРНОЕ ДВИЖЕНИЕ ЖИДКОСТИ.
Задача 8.2
Цена - 100 руб. (pdf) - 120 руб. (word)
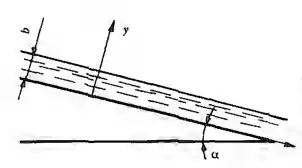
Рисунок 8.2
Слой жидкости (b = 3 мм, ν = 1,5 Ст) равномерно движется под действием силы тяжести по наклонной плоскости, составляющей с горизонтом угол α = 15°. Найти закон распределения скоростей в слое, а также определить расход жидкости, протекающей через поперечное сечение слоя, шириной B = 1 см.
Задача 8.4
Цена - 100 руб. (pdf) - 120 руб. (word)
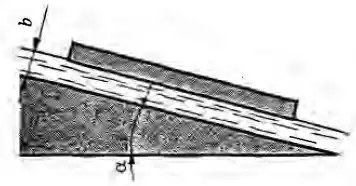
Рисунок 8.4
Пластинка, масса которой m = 0,8 кг и площадь F = 64 см2, сползает по наклонному слою жидкости, толщина которого равна b = 0,5 мм. Определить вязкость жидкости, если скорость равномерного движения пластинки равна u0 = 0,5 м/с, угол наклона плоскости к горизонту α = 12° и плотность жидкости ρ = 900 кг/м3.
Задача 8.5
Цена - 100 руб. (pdf) - 120 руб. (word)
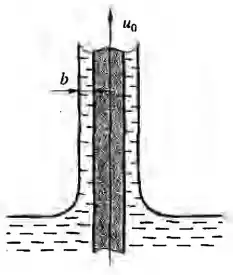
Рисунок 8.5
В подшипнике с кольцевой смазкой слой жидкости подается из масляной ванны к трущимся поверхностям при помощи непрерывно движущегося ремня прямоугольного поперечного сечения. Определить толщину слоя подаваемой смазки и ее количество в секунду, если скорость движения ремня u0 = 0,2 м/с и его ширина равна B = 0,02 м. Динамическая вязкость жидкости μ = 1,5 П, плотность ρ = 900 кг/м3. Построить эпюру скоростей в слое. Указание: Скорость жидкости на границе слоя равна нулю.
Задача 8.7
Цена - 100 руб. (pdf) - 120 руб. (word)
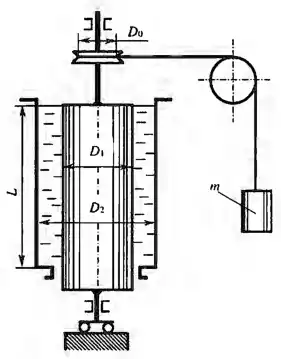
Рисунок 8.7
Вязкость жидкости измеряется на ротационном вискозиметре путем измерения момента трения на внутреннем цилиндре. Определить динамическую вязкость μ, если равномерное вращение внутреннего цилиндра (n = 90 об/мин) достигается с помощью груза массой m = 0,5 кг, а размеры вискозиметра: D0 = 150 мм, D1 = 160 мм, D2 = 200 мм и L = 400 мм. Предварительной тарировкой незаполненного вискозиметра установлено, что момент трения в сальнике и подшипниках при числе оборотов n = 90 об/мин равен Мтр = 0,0735 Н∙м.
Задача 8.8
Цена - 100 руб. (pdf) - 120 руб. (word)
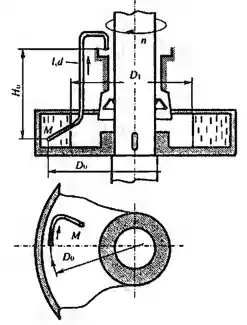
Рисунок 8.8
Для смазки и охлаждения подшипника вертикального вала турбины применен самосмаз, в котором подача жидкости осуществляется при помощи трубки полного напора, введенной в жидкость, заполняющую ковш на валу турбины. Пренебрегая влиянием силы тяжести на распределение давления в ковше, определить, на каком диаметре D0 следует разместить входное отверстие трубки, чтобы в подшипнике был обеспечен расход Q = 0,15 л/с при числе оборотов вала турбины n = 120 об/мин, если ставится условие, чтобы свободная поверхность жидкости в ковше находилась на диаметре D1 = 1 м. Размеры: d = 12 мм; l = 4 м; H0 = 3 м. Вязкость жидкости ν = 0,36 Ст. Учитывать только потери на трение в трубке.
Задача 8.9
Цена - 100 руб. (pdf) - 120 руб. (word)
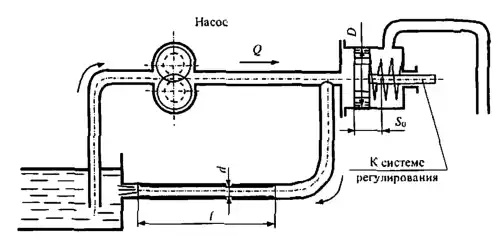
Рисунок 8.9
В регуляторе скорости гидротурбины применен так называемый гидравлический маятник. При изменении числа оборотов регулируемой турбины изменяется расход жидкости, прокачиваемой насосом маятника через калиброванную трубку, вследствие чего изменяется сила давления на поршень, и последний, меняя поджатие пружины, оказывает воздействие на систему регулирования. Определить диаметр и калиброванной трубки так, чтобы при подаче насоса Q = 0,39 л/с (что соответствует рабочему числу оборотов турбины) сжатие пружины было S0 = 60 мм. Жесткость пружины с = 7,5 Н/см, длина трубки l = 0,7 м, вязкость масла 0,3 П. Диаметр поршня D = 30 мм. Сопротивлением подводящих труб пренебречь.
Задача 8.10
Цена - 100 руб. (pdf) - 120 руб. (word)
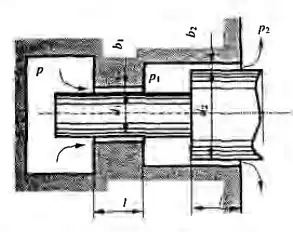
Рисунок 8.10
Жидкость перемещается из области с избыточным давлением р = 0,4 МПа в область, где давление р = 0, последовательно через две кольцевые щели одинаковой длины l = 40 мм. Определить зазор b2 при котором избыточное давление в промежуточной камере было равно р1 = р/2, если d2 = 2d1. Вычислить касательные напряжения τ1, и τ2 на цилиндрических поверхностях, образующих зазоры, а также расход жидкости Q, если d1 = 25 мм, b1 = 0,252 мм, а динамическая вязкости жидкости μ = 10 пуаз.
Задача 8.11
Цена - 100 руб. (pdf) - 120 руб. (word)
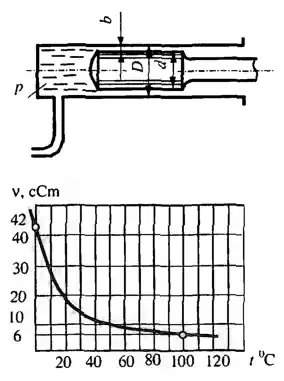
Рисунок 8.11
Во внутренней полости гидроцилиндра поддерживается постоянное избыточное давление P = 2 МПа. Определить наибольший допустимый радиальный зазор b = (D − d)/2 между стенкой цилиндра и плунжером (d = 40 мм, l = 80 мм), если ставится условие, чтобы утечки из полости высокого давления при наибольшем эксцентриситете положения плунжера не превосходили величины (Q = 5 см3/с при температуре масла (АМГ-10), равной t = 100 °С). Как изменятся утечки, если вся конструкция охладится до t0 = 0 °С, и если плунжер выполнен из бронзы (коэффициент линейного расширения α1 = 17,5∙10-6 1/°С), а цилиндр − из стали (α2 = 11,5∙10-6 °С)? Коэффициент вязкости масла АМГ-10 взять из прилагаемого графика. Относительный вес масла принять равным δ = 0,85. Потерями напора на входе и выходе из зазора пренебречь.
Задача 8.12
Цена - 100 руб. (pdf) - 120 руб. (word)

Рисунок 8.12
В межтрубном кольцевом пространстве движется жидкость (μ = 0,9 П) в количестве Q = 0,1 л/с. Определить потерю давления р на длине l = 3 м если D = 15 мм и d = 6 мм. Сравнить ее с потерей в круглой трубе, имеющей равновеликую площадь сечения.
Задача 8.13
Цена - 100 руб. (pdf) - 120 руб. (word)
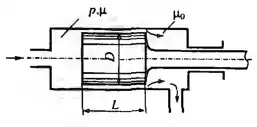
Рисунок 8.13
В рабочей полости гидроцилиндра поддерживается избыточное давление р = 7 МПа. Определить утечки жидкости через кольцевую щель при концентричном расположении поршня в цилиндрическом корпусе, учитывая зависимость вязкости жидкости от давления по формуле (1)
Задача 8.15
Цена - 100 руб. (pdf) - 120 руб. (word)
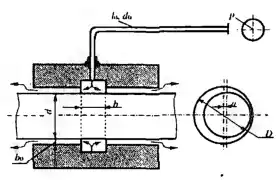
Рисунок 8.15
Масло подается к подшипнику из магистрали по трубке (l0 = 0,8 м, d0 = 6 мм) через кольцевую канавку шириной b = 10 мм, выполненную в средней части подшипника. Длина подшипника l = 120 мм, диаметр вала d = 60 мм, радиальный зазор b0 = 0,1 мм. Избыточное давление масла в магистрали р = 160 кПа, вязкость масла μ = 1,4 П. Принимая режим течения масла в трубке и зазоре ламинарным и пренебрегая влиянием вращения вала, определить количество вытекающего в оба торца масла в двух случаях: 1) вал и подшипник расположены соосно; 2) вал располагается в подшипнике эксцентрично с относительным эксцентриситетом, равным 𝜀=2а/(𝐷−𝑑) = 0,5 где d − диаметр вала, мм; D − диаметр подшипника, мм; а − абсолютный эксцентриситет.
Задача 8.17
Цена - 100 руб. (pdf) - 120 руб. (word)
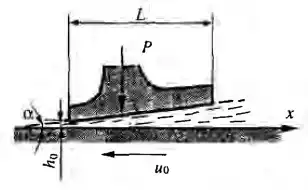
Рисунок 8.17
Башмак пяты способен воспринимать нагрузку благодаря избыточным давлениям, возникающим в клиновидном слое смазки, заполняющем зазор между движущейся опорной поверхностью и наклоненнойк ней поверхностью неподвижного башмака. Рассматривая течение жидкости в слое смазки как плоское, построить эпюру давлений по длине башмака и определить, какую нагрузку он может нести, если скорость движения опорной поверхности равна u0 = 3 м/с и размеры: L = 60 мм, h0 = 0,2 мм; угол установки башмака α = 15°, его ширина (размер в направлении, перпендикулярном плоскости чертежа) B = 150 мм. Вязкость масла 0,8 П.
Задача 8.22
Цена - 100 руб. (pdf) - 120 руб. (word)
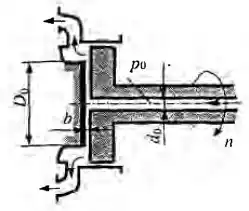
Рисунок 8.22
Гидравлическая пята, частота вращения которой n = 600 об/мин, должна воспринимать осевую нагрузку P = 400 Н. 1) Определить избыточное давление p0, которое необходимо создать в центральном подводящем канале диаметром d0 = 12 мм, если наружный диаметр пяты D0 = 45 мм. 2) Чему равен расход Q жидкости через торцовый зазор пяты, если зазор b = 0,2 мм, динамическая вязкость масла μ = 0,64 П и его плотность ρ = 920 кг/м3.
ГЛАВА 9.
РАСЧЕТ ПРОСТЫХ ТРУБОПРОВОДОВ.
Задача 9.1
Цена - 100 руб. (pdf) - 120 руб. (word)
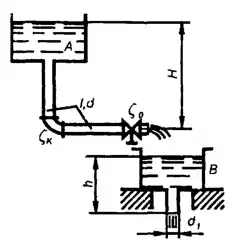
Рисунок 9.1
Вода сливается из бака А в бак В по трубопроводу, диаметр которого d = 80 мм и полная длина L= 2l = 10 м. Из бака В вода вытекает в атмосферу через цилиндрический насадок такого же диаметра d1 = 80 мм (μ = 0,82). Коэффициенты сопротивления колена и вентиля в трубе равны ζк = 0,3 и ζв = 4; коэффициент сопротивления трения λ = 0,03. Определить, какой напор Н нужно поддерживать в баке А, чтобы уровень в баке В находился на высоте h = 1,5 м.
Задача 9.2
Цена - 100 руб. (pdf) - 120 руб. (word)
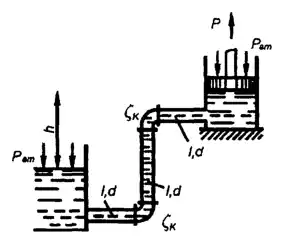
Рисунок 9.2
Поршень диаметром D = 200 мм движется равномерно вверх в цилиндре, засасывая воду из открытого резервуара с постоянным уровнем. Диаметр трубопровода d = 50 мм; длина каждого из его участков l = 4 м; коэффициент сопротивления каждого из колен ζк = 0,5; коэффициент сопротивления трения λ = 0,03. Когда поршень находится выше уровня в резервуаре на h = 2 м, потребная для его перемещения сила равна P = 2350 Н.
Определить скорость подъема поршня и найти, до какой высоты hмакс его можно поднимать с такой скоростью без опасности отрыва от него жидкости, если давление насыщенных паров воды рнп = 4,25 кПа, ее плотность ρ = 995 кг/м3 (t = 30 °С), а атмосферное давление Pат = 98,7 кПа. Массой поршня, трением его о стенки и потерями напора в цилиндре пренебречь.
Задача 9.4
Цена - 100 руб. (pdf) - 120 руб. (word)
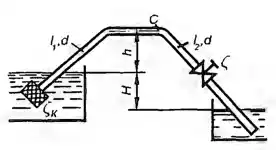
Рисунок 9.4
По сифонному трубопроводу, для которого задан напор H = 6 м, необходимо подавать расход воды Q = 50 л/сек при условии, чтобы вакуум в трубопроводе не превосходил 7 м ст. воды. Опасная точка С расположено выше начального уровня воды на h = 4 м, длина восходящей линии трубопровода до этого сечения l1 = 100 м, а нисходящей линии l2 = 60 м. Трубопровод снабжен приемным клапаном с сеткой (ζк = 5) и задвижкой.
Определить диаметр трубопровода (d и коэффициент сопротивления задвижки ζ удовлетворяющие условиям задачи). Для коэффициента сопротивления трения воспользоваться формулой (9.21), потерями на поворотах пренебречь. Построить график напоров по длине трубопровода.
Задача 9.5
Цена - 100 руб. (pdf) - 120 руб. (word)
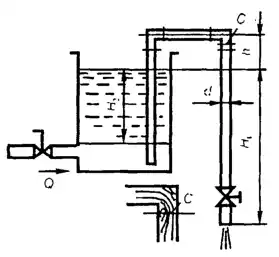
Рисунок 9.5
Определить максимальный расход Q воды, который можно подавать в бак, снабженный сифонной сливной трубой диаметром d = 100 мм и общей длиной L = 10 м, если выходное сечение трубы ниже предельного уровня в баке на Н1 = 4 м. Труба имеет два сварных колена (ζ = 1,3) и вентиль (ζ = 6,9). Коэффициент сопротивления входа в трубу ζвх = 0,5. Коэффициент сопротивления трения λ = 0,025. Определить вакуум рв в сечении С, если это сечение выше предельного уровня на h = 1,5 м и длина участка трубы до него l = 4,5 м. Каков будет вакуум в этом сечении, когда уровень в баке понизится на H2 = 2 м?
Задача 9.6
Цена - 100 руб. (pdf) - 120 руб. (word)
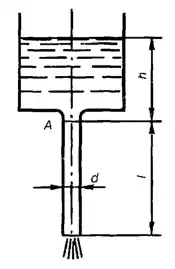
Рисунок 9.6
Жидкость вытекает из открытого бака в атмосферу повертикальной трубе диаметром d = 40 мм.
1. Установить зависимость расхода Q и избыточного давления ри в начальном сечении трубы A от уровня h воды в баке и высоты трубы l.
2. Указать, при каком уровне h давление в сечении А будет равно атмосферному и расход не будет изменяться с высотой трубы.
3. Построить в масштабе графики напоров по высоте трубы при l = 2 м и двух значениях уровня Н = 0,5 и 2 м. Сопротивлением входа в трубу пренебречь, коэффициент сопротивления трения принять λ = 0,04.
Задача 9.7
Цена - 100 руб. (pdf) - 120 руб. (word)
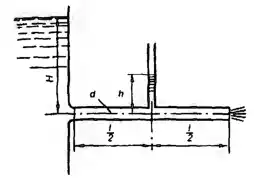
Рисунок 9.7
При истечении воды из большого резервуара в атмосферу по горизонтальной трубе, диаметр которой d = 40 мм и длина l = 10 м, при статическом напоре Н = 10 м получено, что уровень в пьезометре, установленном по середине длины трубы, h = 4,5 м. Определить расход Q и коэффициент сопротивления трения трубы. Сопротивлением входа в трубу пренебречь.
Задача 9.8
Цена - 100 руб. (pdf) - 120 руб. (word)
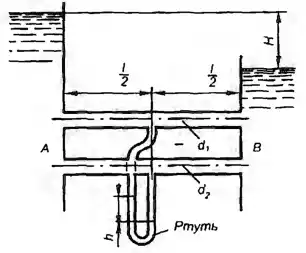
Рисунок 9.8
Резервуары А и В с постоянными уровнями воды соединены двумя параллельными трубами одинаковой длины l = 8 м, диаметры которых d1 = 40 мм и d2 = 10 мм. Определить разность уровней Н в резервуарах и расходы Q1 и Q2 в трубах, если известно, что показание ртутного дифманометра, присоединенного к трубам по середине их длины, равно h = 67 мм. Потерями входа в трубы пренебрегать, значения коэффициента сопротивления трения принять для них равными λ1 = 0,02 и λ2 = 0,04. Построить графики напоров для обеих труб.
Задача 9.9
Цена - 100 руб. (pdf) - 120 руб. (word)
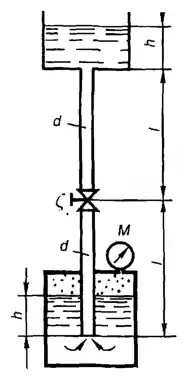
Рисунок 9.9
Вода подается в открытый верхний бак по вертикальной трубе (d = 25 мм; l = 3 м; h = 0,5 м) за счет избыточного давления М в нижнем замкнутом баке. Определить давление М, при котором расход будет равен Q = 1,5 л/с. Коэффициент сопротивления полностью открытого вентиля ζ = 9,3. Коэффициент сопротивления трения определить по заданной шероховатости трубы Δ = 0,2 мм, предполагая наличие квадратичного режима. Построить график напоров по высоте трубы.
Задача 9.10
Цена - 100 руб. (pdf) - 120 руб. (word)
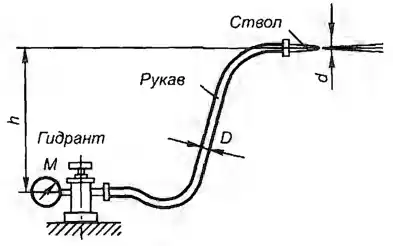
Рисунок 9.10
Какой предельной длины L можно сделать пожарный рукавдиаметром D = 65 мм, если при давлении М = 0,8 МПа (по манометру на гидранте) подача через установленный на конце ствола насадок, выходной диаметр которого d = 30 мм, должна равняться Q = 1,2 м3/мин? Ствол поднят выше манометра на h = 10 м; коэффициент сопротивления ствола с насадком ζ = 0,1 (сжатие струи на выходе отсутствует). Местные потери в рукаве не учитывать. Задачу решить, предполагая, что используются непрорезиненные (λ = 0,054) и прорезиненные (λ = 0,0245) рукава.
Задача 9.11
Цена - 100 руб. (pdf) - 120 руб. (word)
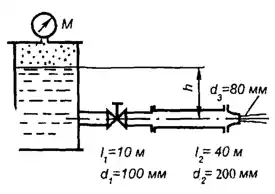
Рисунок 9.11
Для горизонтального трубопровода, размеры которого указаны на схеме, определить расход Q при заданном давлении М = 0,4 МПа и уровне воды в резервуаре h = 5 м. Коэффициенты сопротивления вентиля ζв = 4 и сопла ζс = 0,06 (сжатие струи на выходе из сопла отсутствует). Шероховатость каждого из участков трубопровода Δ = 1 мм (старые водопроводные трубы). Как изменится Q, если диаметр первого участка увеличить до d1 = 200 мм? Построить графики напоров по длине трубопровода.
Задача 9.12
Цена - 100 руб. (pdf) - 120 руб. (word)
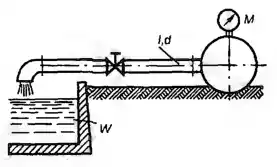
Рисунок 9.12
Наполнение бассейна из магистрали с заданным давлением М = 245 кПа производится по горизонтальной трубе общей длиной l = 45 м, снабженной вентилем (ζв = 4) и отводом (ζот = 0,3). Определить диаметр трубы, который обеспечит наполнение бассейна объемом воды W = 36 м3 за время t = 30 мин. Для коэффициента сопротивления трения воспользоваться формулой: 𝜆 = 0,02/3√d.
Задача 9.13
Цена - 100 руб. (pdf) - 120 руб. (word)
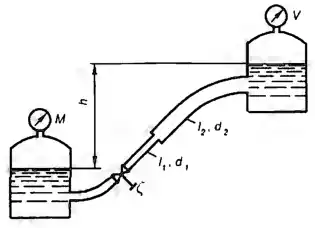
Рисунок 9.13
По трубопроводу размерами l1 = 5 м, d1 = 20 мм и l2 = 5 м, d2 = 40мм подается бензин (ρ = 765 кг/м3, ν = 0,005 Ст) из бака с избыточным давлением М = 90 кПа в расположенный выше бак, где поддерживается вакуум V = 30 кПа; разность уровней в баках h = 6 м. Шероховатость трубопровода Δ = 0,1 мм, коэффициент сопротивления полностью открытого вентиля ζ = 4.
Определить расход бензина и найти значение ζ, при котором расход уменьшится в два раза. В обоих случаях построить графики напоров по длине трубопровода.
Задача 9.15
Цена - 100 руб. (pdf) - 120 руб. (word)
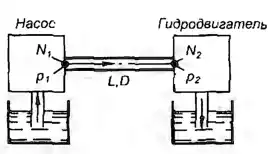
Рисунок 9.15
Мощность N1 = 300 кВт передается потоком воды от насоса к гидродвигателю по горизонтальному трубопроводу длиной l = 1500 м и диаметром D = 400 мм при расходе Q = 0,2 м3/с. Найти величину мощности, теряемой в трубопроводе, принимая коэффициент сопротивления трения λ = 0,03. Какое давление р1 развивает насос в начале трубопровода и каково давление р2 перед гидродвигателем в конце трубопровода?
Указание. Общее выражение мощности потока:
𝑁=𝜌𝑄(𝑝/𝜌 + v2/2 + gz) для данного случая принять z = 0.
Задача 9.16
Цена - 100 руб. (pdf) - 120 руб. (word)
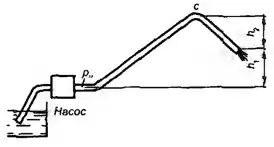
Рисунок 9.16
По напорному стальному трубопроводу диаметром d = 0,3 м и общей длиной L = 50 км вода подается насосом на высоту h1 = 150 м в количестве Q = 6000 м3 за сутки.
1) Определить потерю напора hп в трубопроводе и давление нагнетания рн насоса, учитывая только сопротивление трения, если шероховатость стенок трубопровода Δ = 0,2 мм и кинематический коэффициент вязкости воды ν = 1,3∙10-2 Ст.
2) Найти величину вакуума в сечении С, расположенном выше выходного сечения трубопровода на h2 = 35 м, длина участка трубопровода между этими сечениями l = 10 км.
Задача 9.20
Цена - 100 руб. (pdf) - 120 руб. (word)
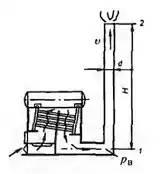
Рисунок 9.20
В котельной установке с естественной тягой при расходе дымовых газов M = 18000 кг/ч вакуум у основания дымовой трубы (обусловленный сопротивлением газового тракта) должен равняться Рв = 20 мм водяного столба. Определить, какую высоту Н должна иметь труба, создающая такой вакуум, если ее диаметр d = 1 м. Средняя плотность дымовых газов ρ1 = 0,6 кг/м3 и окружающего атмосферного воздуха ρ2 = 1,2 кг/м3. Коэффициент сопротивления трения в трубе принять λ = 0,03.
Задача 9.23
Цена - 100 руб. (pdf) - 120 руб. (word)
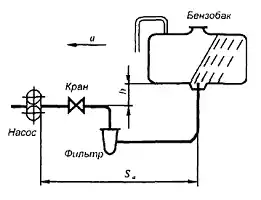
Рисунок 9.23
В топливной системе самолета бензин поступает к насосу из бака с атмосферным давлением по всасывающем трубопроводу общей длиной l = 3 м и диаметром d = 15 мм в количестве Q = 0,2 л/с. В трубопроводе установлены фильтр (ζ = 2) и кран (ζ = 0 при полном открытии). Определить, на какой минимальной глубине h под баком нужно расположить вход в насос, чтобы при полете на высоте 5 км (где атмосферное давление pат = 53,3 кПа) с ускорением a = 12 м/с2 по горизонтали давление на входе в насос было не меньше р2 = 46,7 кПа.
Расстояние по горизонтали от входа в трубопровод до насоса sа = 2 м. Трубопровод рассматривать как гидравлически гладкий, потери на поворотах не учитывать. Относительная плотность бензина δ = 0,72, его кинематическая вязкость ν = 0,007 Ст.
Задача 9.36
Цена - 100 руб. (pdf) - 120 руб. (word)
Сравнить потери напора на трение в круглой и квадратной трубах равной длины и равной площади сечения при одинаковом расходе данной жидкости, предполагая, что в трубах имеет место: 1) ламинарный режим; 2) турбулентный режим (квадратичная область сопротивления), причем шероховатость труб одинакова.
Задача 9.39
Цена - 100 руб. (pdf) - 120 руб. (word)
По горизонтальному трубопроводу длиной L = 17 км необходимо перекачивать нефть (плотность ρ = 920 кг/м3, кинематическая вязкость ν = 0,2 Ст), массовый расход которой M = 200 т/ч, при условии, чтобы падение давления в трубопроводе не превышало ΔP = 4 МПа. Шероховатость трубопровода Δ = 0,2 мм. Определить диаметр трубопровода.
Задача 9.46
Цена - 100 руб. (pdf) - 120 руб. (word)
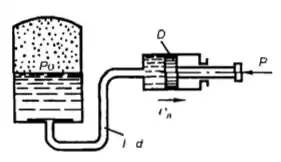
Рисунок 9.46
В системе объемного гидропривода пневмогидравлический аккумулятор с избыточные давлением воздуха Р0 = 5 МПа питает маслом гидроцилиндр диаметром D = 60 мм. Плотность и кинематическая вязкость масла ρ = 910 кг/м3, ν = 0,2 Ст. Соединительная латунная трубка (шероховатость Δ = 0,01 мм) имеет размеры l = 12 м и d = 15 мм. Определить скорость υп установившегося движения поршня гидроцилиндра, когда к нему приложена полезная нагрузка P = 12 кН. Какой станет скорость поршня при сбросе полезной нагрузки (P = 0)? Местные сопротивления трубки (вход, повороты и арматура) принять равными 30 % от сопротивления трения по ее длине. Утечками и трением поршня в гидроцилиндре пренебречь.
Задача 9.49
Цена - 100 руб. (pdf) - 120 руб. (word)
Найти отношение потерь напора в данной трубе при турбулентном и ламинарном режимах течения данной жидкости, расходы которой в обоих случаях одинаковы. Расчет выполнить для значения числа Рейнольдса Rе = 105, предполагая трубу при турбулентном режиме гидравлически гладкой.
ГЛАВА 10.
РАСЧЕТ СЛОЖНЫХ ТРУБОПРОВОДОВ.
Задача 10.1
Задача 10.1
Цена - 100 руб. (pdf) - 120 руб. (word)
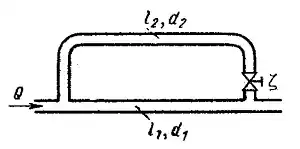
Рисунок 10.1
Найти как распределяется расход Q = 25 л/с между двумя параллельными трубами, одна из которых имеет длину l1 = 30 м, диаметр d1 = 50 мм, а другая (с задвижкой, коэффициент сопротивления которой ξ = 3) имеет длину l2 = 50 м и диаметр d2 = 100 мм. Какова будет потеря напора hn в разветвленном участке? Значения коэффициентов сопротивления трения труб принять соответственно равными λ1 = 0,04 и λ2 = 0,03.
Задача 10.8
Цена - 100 руб. (pdf) - 120 руб. (word)
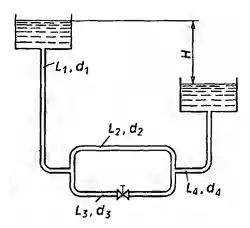
Рисунок 10.8
Определить расход воды в системе труб, соединяющих два резервуара с разностью уровней Н = 24 м, если размеры труб L1 = L2 = L3 = L4 = 100 м, d1 = d2 = d4 = 100 мм, d3 = 200 мм Значения коэффициента сопротивления трения в трубах λ1 = λ2 = λ4 = 0,025, λ3 = 0,02 и коэффициента сопротивления задвижки ζ = 30. Как повлияет на величину расхода закрытие задвижки?
Задача 10.14
Цена - 100 руб. (pdf) - 120 руб. (word)
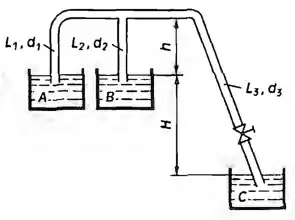
Рисунок 10.14
Из резервуаров А и В с одинаковыми уровнями вода по трубам L1 = 200 м, d1 = 200 мм и L2 = 100 м, d2 = 100 мм поступает в магистральную трубу длиной L3 = 600 м, диаметром d3 = 200 мм, а затем сливается в резервуар С.
1. Определить расход Q3 воды, поступающей в резервуар С при напоре H = 16 м и коэффициенте сопротивления задвижки ζ = 12.
2. Чему равен (при том же напоре Н) минимальный коэффициент сопротивления задвижки, если минимальное абсолютное давление в системе принять равным нулю?
Длина горизонтального участка трубы 3 равна 160 м, высота его расположения над уровнями h = 4 м. Принять λ1 = λ3 = 0,02; λ2 = 0,025.
Кроме потерь в задвижке, другие местные потери напора не учитывать. Атмосферное давление принять равным 98 кПа.
Задача 10.29
Цена - 100 руб. (pdf) - 120 руб. (word)
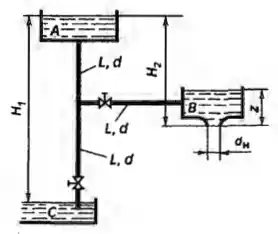
Рисунок 10.29
Из бака А с постоянным уровнем вода поступает в баки В и С по одинаковым трубам L = 100 м, d = 50 мм (λ = 0,03). Из бака В вода вытекает в атмосферу через сходящийся насадок диаметрами dн = 25 мм (ξ = 0,04, ε = 1) при постоянном напоре z. Определить расходы в каждой из труб при напорах H1 = 15 м и H2 = 10 м и полностью открытых кранах (ξ = 0).
Какими станут расходы и напор z, если полностью закрыть кран на трубе, ведущей в бак С?
Задача 10.41
Цена - 100 руб. (pdf) - 120 руб. (word)
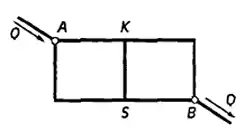
Рисунок 10.41
Трубы, составляющие кольцевой разветвленный участок, имеют следующие размеры: LAS = 300 м; dAS = 75 мм; LAK = 250 м; dAK = 100 мм; LKB = 100 м; dKB = 75 мм; LSB = 265 м; dSB = 100 мм; LKS = 100м; dKS = 75 мм. Перепад напоров в узлах A и B участка HAB = 12 м. Определить расходы в трубах и потери напора в них, принимая коэффициент сопротивления трения в трубах λ = 0,032.
ГЛАВА 11.
ИСТЕЧЕНИЕ ПОД ПЕРЕМЕННЫМ НАПОРОМ.
Задача 11.5
Задача 11.5
Цена - 100 руб. (pdf) - 120 руб. (word)
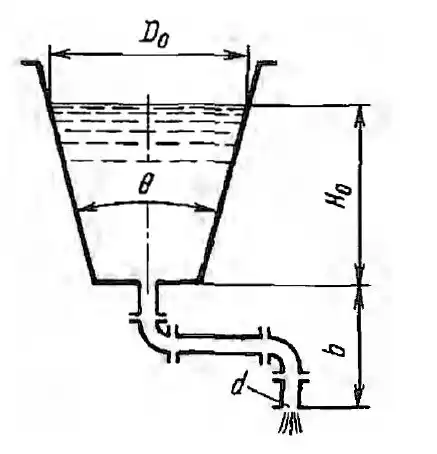
Рисунок 11.5
Определить время опорожнения конического сосуда (θ = 30°), если опорожнение происходит через трубу, диаметр которой d = 15 мм и суммарный коэффициент сопротивления ζ = 2,5. Начальный уровень жидкости H0 = 0,85 м; D0 = 1 м; вертикальное расстояние от выходного отверстия трубы до дна сосуда b = 0,6 м.
ГЛАВА 14.
РАБОТА НАСОСОВ НА СЕТЬ.
Задача 14.4
Задача 14.4
Цена - 100 руб. (pdf) - 120 руб. (word)
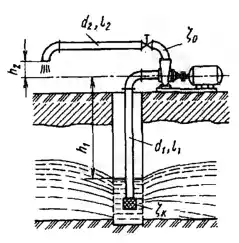
Рисунок 14.4
Центробежный насос откачивает грунтовую воду из колодца в количестве Q = 40 л/с. При этом горизонт воды в колодце устанавливается на h1 = 5 м.
1. Определить диаметр d1 всасывающей трубы насоса, при которой вакууметрическая высота при входе в насос не превосходит 7 м. Длина всасывающей трубы l1 = 8 м.
2. Найти мощность Nдв при полностью открытой задвижке на нагнетательной трубе, имеющей длину l2 = 5 м и диаметр d2 = 150 мм, если выходное сечение ее расположено на h2 = 0,6 м выше оси насоса; КПД насоса η = 0,7.
При расчете принять коэффициент сопротивления трения трубопроводов λ = 0,03, коэффициент сопротивления каждого отвода ξ0 = 0,4, коэффициент сопротивления всасывающей коробки с обратным клапаном ξк = 5.
Задача 14.11
Цена - 100 руб. (pdf) - 120 руб. (word)
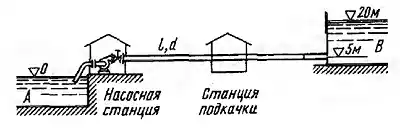
Рисунок 14.11
Насосная станция перекачивает воду в количестве QН1 = 0,6 м3/сек по горизонтальному трубопроводу длиной l = 5 км и диаметром d = 500 мм из бассейна А в резервуар В. Определить мощность насоса, установленного на насосной станции, учитывая в трубопроводе только потери трения (λ = 0,015). Определить, где и какой мощности надо установить станцию подкачки, чтобы по тому же трубопроводу увеличить подачу до QН2 = 0,9 м3/сек, обеспечивая по всей длине трубопровода избыточное давление не менее 0,5 атм и считая, что при увеличении расхода напор насоса на насосной станции в соответствии с его характеристикой уменьшится на 15 %. В обоих случаях построить пьезометрические линии для системы.
Задача 14.24
Цена - 100 руб. (pdf) - 120 руб. (word)
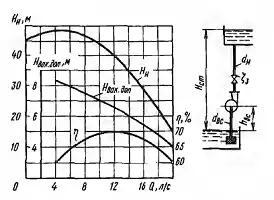
Рисунок 14.24
В насосной установке вода подается на высоту Hст = 15 м центробежным насосом с заданной характеристикой при высоте всасывания hвс = 4 м. Напорная и всасывающая трубы имеют диаметры dн = 80 мм и dвс = 100 мм. Суммарный коэффициент сопротивления напорной трубы (без учета задвижки на выходе из насоса) ζн = 22 и всасывающей трубы ζвс = 6. Определить наибольшую подачу насоса, допустимую по условиям всасывания им жидкости. При каком наименьшем значении коэффициента сопротивления задвижки ζз будет достигнута эта подача? Какую мощность будет потреблять насос на этом предельном режиме?
Задача 14.29
Цена - 100 руб. (pdf) - 120 руб. (word)
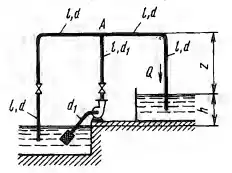
Рисунок 14.29
Центробежный насос перекачивает воду по трубопроводу (l = 5 м, d1 = 75 мм), который в точке А разветвляется на две линии диаметром d = 50 мм и длиной 2l каждая. Расход в правой ветви Q = 10 л/с, а высоты равны h = 1 м, z = 4 м. Определить мощность насоса Nн, принимая коэффициент сопротивления трения в трубах λ = 0,03, суммарный коэффициент сопротивления всасывающей линии ξвс> = 4 и пренебрегая потерями и задвижках. Указать сечение трубопровода, в котором имеет места наименьшее давление.

