
Решебник по курсу "Гидродинамика" НГАСУ
Учебные Задания. Новосибирск 1988 г.
специальность "Теплогазоснабжение и вентиляция"

I. Основные физические свойства газов и жидкостей (Задачи 1-9).
Задача 1
Цена - 80 руб. (pdf) - 100 руб. (word)
Задача 1. Тело с характерным линейным размером L = 1 м движется в газовой среде, причем средняя длина свободного пробега молекул газа 𝑙 = 10𝑓(𝑁), где 𝑓(𝑁) = 1−11∙𝑠𝑖𝑛2𝜋𝑁/20 Пригодна ли для описания обтекания тела газом модель сплошной среды?
Исходные данные: N = 16; 𝑓(𝑁) = 1−11∙𝑠𝑖𝑛2𝜋∙16/20 = 1−11∙𝑠𝑖𝑛2(0,8∙𝜋)
Задача 2
Цена - 80 руб. (pdf) - 100 руб. (word)
Задача 2. N литров воды весят 0,96N + 0,04 кгс. Определить плотность и удельный вес воды в физической, технической и интернациональной системах единиц. Какова температура воды?
Исходные данные: N = 16; V = N = 16л; Р = 0,96·16 + 0,04 = 15,4кгс
Задача 3
Цена - 80 руб. (pdf) - 100 руб. (word)
Задача 3. Определить массу и вес воздуха в комнате, размером 2,5 х 4 х 6 м при атмосферном давлении, если температура воздуха t = 0,25N + 5 °C.
Исходные данные: N = 16; t = 0,25·16 + 5 = 9 °C.
Задача 4
Цена - 80 руб. (pdf) - 100 руб. (word)
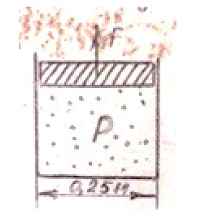
Задача 4. Давление газа в цилиндрическом сосуде равно Р = 1 + 0,5N атм. Определить силу, действующую на поршень со стороны газа в технической, и международной системе единиц.
Исходные данные: N = 16; Р = 1 + 0,5·16 = 9 атм.
Задача 5
Цена - 80 руб. (pdf) - 100 руб. (word)
Задача 5. При опрессовке трубопровода длиной l и диаметром D = 250 мм давление воды поднято от атмосферного до Р2 = 10 + 0,1N атм. Какой объем воды потребовалось подать в трубопровод за время подъема давления до назначенной величины? Расширение трубы не учитывать.
Исходные данные: N = 16; Р2 = 10 + 0,1·16 = 11,6 атм.
Задача 6
Цена - 80 руб. (pdf) - 100 руб. (word)
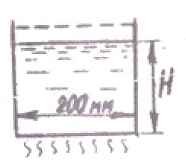
Задача 6. В открытый цилиндрический сосуд диаметром d = 200 мм залита вода температурой t1 = 4 °C до уровня H = 100 + N см. На сколько поднимется уровень воды при нагревании ее до t2 = 70 + 0,3N °C? Какова при этом будет ее плотность? Тепловым расширением сосуда и испарением с поверхности пренебречь.
Исходные данные: N = 16; t2 = 70+0,3·16 = 74,8°C; Н = 100+16 = 116 см.
Задача 7
Цена - 80 руб. (pdf) - 100 руб. (word)
Задача 7. Замкнутый сосуд полностью заполнен водой при температуре t1 = 4°C и давлении 1 атм. Каким будет давление в жидкости при повышении температуры до t2 = 5 + 0,1N °C? Расширением стенок сосуда пренебречь. Решить эту же задачу, при условии, что вместо воды в сосуде заключен воздух.
Исходные данные: N = 16; t2 = 5 + 0,1·16 = 6,6 °C.
Задача 8
Цена - 80 руб. (pdf) - 100 руб. (word)
Задача 8. При измерении поля скоростей в жидкости у стенки трубы было установлено, что скорость жидкости возрастает на dv/dx = 1 + 0,01N см/с с удалением от стенки на каждый миллиметр. Определить касательное напряжение вязкого трения, если движущаяся жидкость – вода при температуре t = 10 + 0,3N °C? Решить эту же задачу для воздуха.
Исходные данные: N = 16; dv/dx = 1 + 0,01·16 = 1,16 (см/с)/мм; t = 10 + 0,3·16 = 14,8 °C.
Задача 9
Цена - 80 руб. (pdf) - 100 руб. (word)
Задача 9. Вычислить действительные давления по показаниям жидкостного манометра (вода-стекло) и вакуумметра (ртуть-стекло), если диаметр трубок d = 4 мм, а отсчеты по шкалам, соответственно hводы = 10 + N, см, hртути = 10 + 0,2N, см.
Исходные данные: N = 16; hводы = 10 + 16 = 26 см; hртути = 10 + 0,2·16 = 13,2 см.
II. Гидроаэростатика (Задачи 10-24).
Задача 10
Цена - 80 руб. (pdf) - 100 руб. (word)
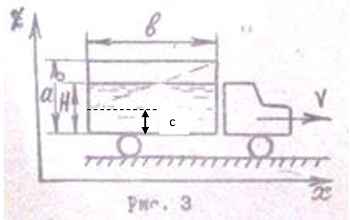
Задача 10. Автомобиль, везущий прямоугольный открытый бак с жидкостью, движется со скоростью V = 75 км/ч. Размеры бака: a = 1,6 м; b = 4 м; уровень жидкости Н = 0,9 + 0,005N. Определить минимально допустимое время торможения автомобиля, при котором жидкость не будет переливаться через край. Процесс торможения считать равнозамедленным.
Исходные данные: N = 16; Н = 0,9 + 0,005∙16 = 0,98 м.
Задача 11
Цена - 100 руб. (pdf) - 130 руб. (word)
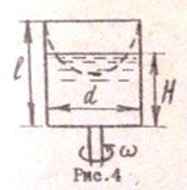
Задача 11. В цилиндрический сосуд с диаметром d = 200 мм высотой l = 300 мм налита жидкость до уровня Н = 15 + 0,14∙N, см. Сосуд начинает вращаться. Определить, при какой угловой скорости ω жидкость начнет выплескиваться через край сосуда.
Исходные данные: N = 16; Н = 15 + 0,14∙16 = 17,24 см = 0,1724 м.
Задача 12
Цена - 80 руб. (pdf) - 100 руб. (word)
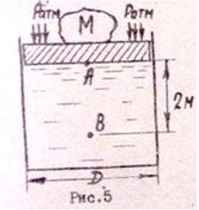
Задача 12. Определить величину внешнего, полного и избыточного гидростатического давления в точках А и В, если на поршень массой m = 10 кг и диаметром d = 0,1 + 0,002N м положен груз массой М = 10 + 0,4N кг, а плотность жидкости равна 1000 кг/м3.
Исходные данные: N = 16; d = 0,1 + 0,002·16 = 0,132 м; М = 10 + 0,4·16 = 16,4 кг.
Задача 13
Цена - 80 руб. (pdf) - 100 руб. (word)
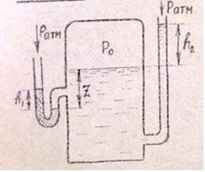
Задача 13. В закрытом резервуаре с водой при t = 20 ºC давление газа над поверхностью равно Р0. Определить величину Р0 и пьезометрическую высоту h2, если показание ртутного манометра h1 = 10 + 0,5N, см, Z = 1 + 0,01N, м.
Исходные данные: N = 16; h1 = 10 + 0,5∙16 = 18 см = 0,18 м; Z = 1 + 0,01∙16 = 1,16 м.
Задача 14
Цена - 100 руб. (pdf) - 130 руб. (word)
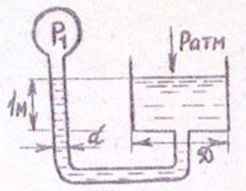
Задача 14. Колено диаметром d = 5 см соединяет резервуар с воздухом под давлением Р1 с открытым цилиндрическим сосудом диаметром D = 6 + 0,1N, см. Первоначальное давление Р1 равно атмосферному. На сколько нужно увеличить давление Р1, чтобы вода в левом колене опустилась на 1 м? Как зависит это приращение от D? Построить график.
Исходные данные: N = 16; D = 6 + 0,1∙16 = 7,6 см.
Задача 15
Цена - 80 руб. (pdf) - 100 руб. (word)
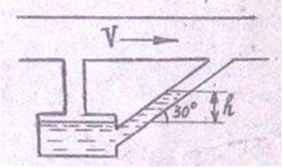
Задача 15. Для измерения давления в вентиляционной трубе применяется наклонный микроманометр, заполненный спиртом (γ = 7,85 кН/м3). Угол наклона трубки равен 30°. Определить длину шкалы для измерения падения давления порядка Рмах = 1000+30·N.
Исходные данные: N = 16; Рмах = 1000 + 30·16 = 1480 Па.
Задача 16
Цена - 100 руб. (pdf) - 130 руб. (word)

Задача 16. Определить силу давления на щит, шириной b = 5 м, если Н1 = 2+0,05N, Н2 = 2 м, α = 60°. Построить эпюру избыточного гидростатического давления.
Исходные данные: N = 16; Н1 = 2 + 0,05·16 = 2,8 м.
Задача 17
Цена - 80 руб. (pdf) - 100 руб. (word)
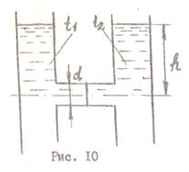
Задача 17. Два стояка водяного отопления соединены горизонтальным участком с задвижкой диаметром d = 500 мм, Температура воды в стояках t1 = 4 °C и t2 = 80 °С. Найти результирующую силу давления на задвижку, если h = 3 + 0,1N, м.
Исходные данные: N = 16; h = 3 + 0,1·16 = 4,6 м.
Задача 18
Цена - 150 руб. (pdf) - 180 руб. (word)
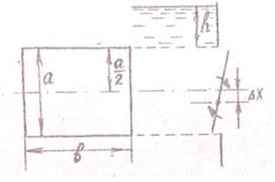
Задача 18. Для регулирования уровня воды в открытом резервуаре применен поворачивающийся щиток, который должен автоматически открывать прямоугольное отверстие размером aхb. Ось щитка расположена на Δх см ниже его центра тяжести. Какова будет сила давления воды на щиток при a = 200 мм, b = 500 мм, h = 0,1 + 0,01N, м? При какой глубине h откроется щиток, если Δх = 65 – 0,6N, мм?
Исходные данные: N = 16; h = 0,1 + 0,01·16 = 0,26 м; Δх = 65 – 0,6·16 = 55,4 мм.
Задача 19
Цена - 80 руб. (pdf) - 100 руб. (word)
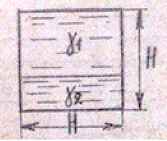
Задача 19. В бак квадратного сечения налиты две несмешивающиеся жидкости. Более тяжелая жидкость заполняет бак на 1/3 его высоты. Н = 1 + 0,1N. Определить полное давление на торцевую стенку если γ1 = 7 + 0,2·N кН/м3, γ2 = 10 кН/м3.
Исходные данные: N = 16; Н = 1 + 0,1N = 1 + 0,1·16 = 2,6 м; γ1 = 7 + 0,2·16 = 10,2 кН/м3.
Задача 20
Цена - 100 руб. (pdf) - 130 руб. (word)
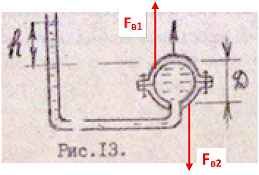
Задача 20. Определить силу, действующую на болты шара, диаметром D = 500 мм, заполненного водой, если по трубке жидкость поднялась на величину h = 1 + 0,1N.
Исходные данные: N = 16; h = 1 + 0,1·16 = 2,6 м.
Задача 21
Цена - 80 руб. (pdf) - 100 руб. (word)
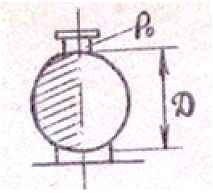
Задача 21. Металлическая цистерна имеющая диаметр D = 2 м и длину l = 10 м заполнена жидкостью с плотностью ρ = 800 + 2N. Давление на поверхности жидкости Р0 равно атмосферному. Определить силу давления жидкости на левую половину цистерны.
Исходные данные: N = 16; ρ = 800 +2·16 = 832 кг/м3.
Задача 22
Цена - 80 руб. (pdf) - 100 руб. (word)
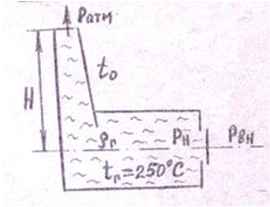
Задача 22. Определить разность давления Рн – Рвн в топке котла и перед топочной заслонкой (тягу дымовой трубы), если высота дымовой трубы Н = 30 м, плотность дымовых газов ρг = 0,58 кг/м3, а температура наружного воздуха t0 = 30 – 0,6N, °С.
Исходные данные: N = 16; t0 = 30 – 0,6·16 = 20,4 °С.
Задача 23
Цена - 80 руб. (pdf) - 100 руб. (word)
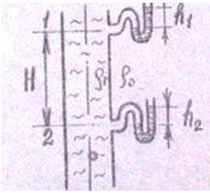
Задача 23. К газовому стояку на отметках 1 и 2 присоединены водяные манометры, показания которых h1 и h2 соответственно. Показание какого манометра будет больше и на сколько, если плотность газа ρг = 0,7 + 0,15N кг/м3, плотность воздуха ρo = 1,2 кг/м3.
Исходные данные: N = 16; ρг = 0,7 + 0,015·16 = 0,31 кг/м3.
Задача 24
Цена - 80 руб. (pdf) - 100 руб. (word)
Задача 24. Определить давление и температуру в атмосфере на высоте h = 1000 + 10N метров, если у поверхности земли давление составляет 750 мм.рт.ст и температура 20 °С.
Исходные данные: N = 16; h = 1000 + 10·16 = 1160 м.
III. Кинематика (Задачи 25-30).
Задача 25
Цена - 80 руб. (pdf) - 100 руб. (word)
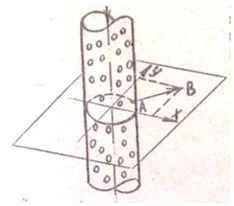
Задача 25. В дырчатый трубопровод радиуса R0 нагнетается воздух, который выходит в отверстия равномерно и прямолинейно. Траектория перемещения произвольной частицы жидкости в плоскости, перпендикулярной оси трубы описывается соотношением 𝑥 = 𝑥0√1+𝑘𝑡; 𝑦 = 𝑦0√1+𝑘𝑡 (1) где x0 и y0 координаты частиц жидкости при t = 0, т.е. в момент выхода из отверстий на окружности трубопровода. Какова будет скорость вытекающего воздуха на расстоянии 1 м от оси трубы, если R0 = 0,2 м, k = 50 + N с-1. Определить поле скоростей Vx и Vy.
Исходные данные: N = 16; k = 50 + 16 = 66 с-1.
Задача 26
Цена - 80 руб. (pdf) - 100 руб. (word)

Задача 26. Для условий задачи 25 определить, возможен ли переход от эйлеровых координат к лагранжевым и обратно, и почему? Что происходит с жидкостью – растяжение или сжатие? Во сколько раз изменится плотность частицы через 5 с после полета?
Исходные данные: N = 16; k = 50 + 16 = 66 с-1.
заказать
Задача 27
Цена - 80 руб. (pdf) - 100 руб. (word)

Задача 27. Для условий задачи 25 доказать, что движение воздуха в плоскости XY будет потенциальным. Найти потенциал течения, функцию тока и нарисовать гидродинамическую сетку.
Исходные данные: N = 16; k = 50 + 16 = 66 с-1.
заказать
Задача 28
Цена - 80 руб. (pdf) - 100 руб. (word)
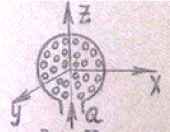
Задача 28. Воздух нагнетается в пустотелый шарик, в поверхности которого устроено большое количество отверстий. Через отверстия воздух выходит во все стороны равномерно и прямолинейно. Общий расход Q = 20 + 0,2N м3/с. Каким будет движение воздуха – вихревым или потенциальным?
Исходные данные: N = 16; Q = 20 + 0,2·16 = 23,2 м3/с.
Задача 29
Цена - 80 руб. (pdf) - 100 руб. (word)
Задача 29. Для условий задачи 25 написать тензор скоростей деформации и охарактеризовать деформационное движение вдоль оси х.
Исходные данные: N = 16; k = 50 + 16 = 66 с-1.
Задача 30
Цена - 80 руб. (pdf) - 100 руб. (word)

Задача 30. При вытекании жидкости в отверстии образовалась вихревая трубка в виде воронки с диаметром горловины d = 1 см. Замеры на расстоянии R = 1 м от центра отверстия показали, что скорость на окружности с радиусом R равна V = 20 + 0,3N см/с и направлена под углом α = 5 + 0,25N град к касательной. Считая движение плоским, определить интенсивность вихревой трубки, линейную скорость Vт жидкости на поверхности вихревой трубки и среднюю угловую скорость вихревой трубки.
Исходные данные: N = 16; V = 20 + 0,3·16 = 24,8 см/с; α = 5 + 0,25·16 = 9°.
IV. Динамика установившегося движения. Уравнение Бернулли (Задачи 31-39).
Задача 31
Цена - 100 руб. (pdf) - 130 руб. (word)

Задача 31. По трубе диаметром d = 2 см движется сжатый воздух. На выходе трубы (сечение 2) давление Р2 равно атмосферному, а скорость движения воздуха V2 = 5 + 0,05N м/с. Определить массовый расход. Какова будет скорость в начале трубы (сечение 1), если давление там равно Р1 = 1,5 + 0,1N атм? Течение считать изотермическим при t = 20 °C.
Исходные данные: N = 16; V2 = 5 + 0,05∙16 = 5,8 м/с; Р1 = 1,5 + 0,1∙16 = 3,1 атм.
Задача 32
Цена - 80 руб. (pdf) - 100 руб. (word)
Задача 32. Из стеклянной трубы диаметром d = 5 см за t = 10 секунд вылилось m = 200 + 3N г воды. Считая движение ламинарным, определить скорость движения воды на оси трубы, если tводы = 20 °C.
Исходные данные: N = 16; m = 200 + 3∙16 = 248 г.
Задача 33
Цена - 80 руб. (pdf) - 100 руб. (word)
Задача 33. Конденсатор паровой турбины, установленный на тепловой электростанции, оборудован n = 8186 охлаждающими трубками диаметром d = 20 мм. В нормальных условиях работы через конденсатор пропускается расход Q = 12000 + 100N м3/час циркуляционной воды с температурой t = 10 °C. Определить режим течения в трубах.
Исходные данные: N = 16; Q = 12000 + 100∙16 = 12160 м3/час.
Задача 34
Цена - 80 руб. (pdf) - 100 руб. (word)
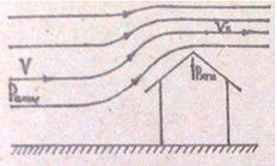
Задача 34. Определить силу, стремящуюся поднять крышу при скорости ветра на некотором расстоянии от здания V = 21 + 0,2N м/с, а над коньком крыши Vк = V(1,5 + 0,01N). Площадь горизонтальной проекции крыши S = 60 м2, вес крыши G = 2,5 т.
Исходные данные: N = 16; V = 21 + 0,2∙16 = 24,2 м/c; Vк = V(1,5 + 0,01∙16) = 40,17 м/с.
Задача 35
Цена - 100 руб. (pdf) - 130 руб. (word)
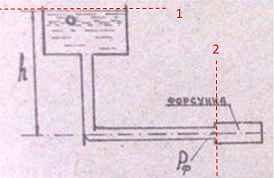
Задача 35. Нагревательная печь расходует m = 200 + 20N кг мазута в час. Плотность мазута ρ = 900 кг/м3, кинематическая вязкость ν = 0,27 см2/с. Определить, на какой высоте h следует расположить напорный бак относительно оси форсунки, если избыточное давление перед ней Рф должно быть не менее 50 кПа при длине подводящей трубы l = 25 м и диаметре d = 20 мм. местными потерями пренебречь.
Исходные данные: N = 16; m = 200 + 20∙16 = 520 кг/час.
Задача 36
Цена - 150 руб. (pdf) - 180 руб. (word)
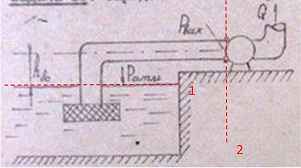
Задача 36. Определить наибольшую высоту всасывания hвс центробежного насоса (центра колеса), с учетом и без учета потерь на все гидравлические сопротивления если расход насоса Q = 10 + 0,5N л/с, диаметр трубы d = 200 мм, длина всасывающей трубы l = 10 + 0,2N м. Величина вакуума в отсасывающей трубе Рвак не должна превосходить 0,6 атм. Вычислить эквивалентную длину при Δэ = 0,1 мм.
Исходные данные: N = 16; Q = 10 + 0,5∙16 = 18 л/с;
l = 10 + 0,2·16 = 13,2 м.
Задача 37
Цена - 250 руб. (pdf) - 300 руб. (word)
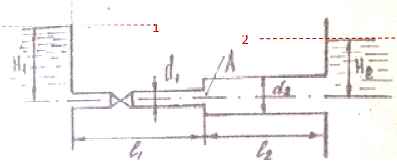
Задача 37. Определить расход и скорость воды в трубах, если Н1 = 1 + 0,05 N м; Н2 = 0,5 м; l1 = м; l2 = 4 м; d1 = 20 мм; d2 = 40 мм; Трубы стальные не новые, коэффициент сопротивления вентиля принять равным ζв = 8. Построить линию пьезометрического и гидродинамического напоров. Определить давление в начале 2-й трубы (точка А).
Исходные данные: N = 16; Н1 = 1 + 0,05∙16 = 1,8 м.
Задача 38
Цена - 250 руб. (pdf) - 300 руб. (word)
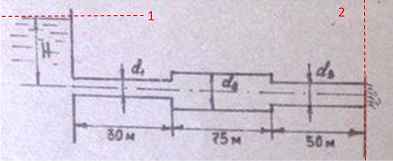
Задача 38. Определить расход и скорость воды в каждой трубе, с учетом и без учета потерь на все гидравлические сопротивления если d1 = 100 мм; d2 = 200 мм; d3 = 150 мм; а напор Н = 4 + 0,1N м. Вычислить эквивалентную длину при Δэ = 0,1 мм. Построить линию пьезометрического и гидродинамического напоров.
Исходные данные: N = 16; Н = 4 + 0,1∙16 = 5,6 м.
Задача 39
Цена - 200 руб. (pdf) - 250 руб. (word)
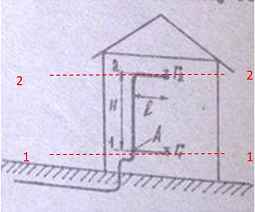
Задача 39. Газ по домовому газопроводу подается на отметку 1 к горелке Г1 и на отметку 2 к горелке Г2. Определить массовый расход газа в каждой горелке, если Н = 10 + 0,1N м, l = 2 м; d = 25 мм; манометрическое давление в точке А равно РмА = 20 Па. Трубы стальные не новые, эквивалентная длина местных сопротивлений при подаче газа от точки А до горелки Г2 равна lэкв = 15 м, коэффициент сопротивления горелки ζ = 20, плотность наружного воздуха ρв = 1,2 кг/м3, плотность газа ρг = 0,7 кг/м3, вязкость газа ν = 12·10-6 м2/с.
Исходные данные: N = 16; Н = 10 + 0,1∙16 = 11,6 м.
V. Гидравлический расчет трубопроводов (Задачи 40-48).
Задача 40
Цена - 150 руб. (pdf) - 180 руб. (word)
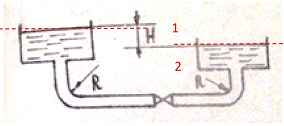
Задача 40. Два резервуара соединены трубой диаметром d = 100 мм, длиной l = 50 м, с эквивалентной шероховатостью Δэ = 0,1 мм. Определить, при какой разности уровней воды в этих резервуарах расход воды будет Q = 5 + 0,25N л/с. Коэффициент вязкости воды 𝜈 = 0,0131 см2/с, радиус поворота R = 200 мм, коэффициент сопротивления вентиля ζв = 3.
Исходные данные: N = 16; Q = 5 + 0,25∙16 = 9 л/с.
Задача 41
Цена - 100 руб. (pdf) - 130 руб. (word)
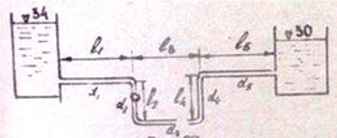
Задача 41. Определить потери напора и необходимость насосной установки для водопровода из последовательно соединенных чугунных труб, если расход воды Q = 1 + 0,05∙16 л/с и температура t = 20 °C а размеры труб: l1 = 50 м; d1 = 100 мм; l2 = 30 м; d2 = 100 мм; l3 = 150 м; d3 = 50 мм; l4 = 30 м; d4 = 50 мм; l5 = 60 м; d5 = 50 мм.
Исходные данные: N = 16; Q = 1 + 0,05∙16 = 1,8 л/с.
Задача 42
Цена - 80 руб. (pdf) - 100 руб. (word)
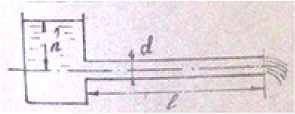
Задача 42. Определить диаметр стальной трубы, бывшей в употреблении, чтобы при заданном напоре h = 40 м и длине трубы l = 100 м пропустить расход воды Q = 0,01∙N м3/с.
Исходные данные: N = 16; Q = 0,01∙16 = 0,16 м3/с.
Задача 43
Цена - 100 руб. (pdf) - 130 руб. (word)

Задача 43. Для увеличения пропускной способности водопровода диаметром d1 = 100 мм к нему параллельно присоединена труба с диаметром d2 = 200 мм. Определить расходы в первой и второй трубках соответственно, если общий расход Q = 5 + 0,5∙N л/с.
Исходные данные: N = 16; Q = 5 + 0,5∙16 = 13 л/с.
Задача 44
Цена - 150 руб. (pdf) - 180 руб. (word)
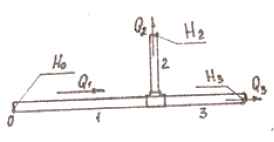
Задача 44. Определить расходы Q1, Q2, Q3 в трубах системы, если напор в точке 0 равен Н0 = 15 + 0,1N м, напоры на концах труб 2 и 3 равны Н2 = Н3 = 12 м. Трубы стальные не новые. l1 = 200 м; d1 = 200 мм; l2 = 100м; d2 = 100 мм; l3 = 50 м; d3 = 100 мм.
Исходные данные: N = 16; V = 21 + 0,2∙16 = 24,2 м/c; Vк = V(1,5 + 0,01∙16) = 40,17 м/с.
Задача 45
Цена - 100 руб. (pdf) - 130 руб. (word)
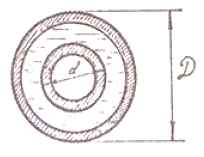
Задача 45. Вода при температуре t = 10 °C и в количестве Q = 0,05 + 0,005∙N м3/с движется в горизонтальной трубе кольцевого сечения, состоящей из двух концентрических оцинкованных труб. Внутренняя труба имеет наружный диаметр d = 104 мм, а наружная труба имеет внутренний диаметр D = 400 мм. Найти потери напора на трение, при длине трубы, равной L = 500 м.
Исходные данные: N = 16; Q = 0,05 + 0,005∙16 = 0,13 м3/с.
Задача 46
Цена - 80 руб. (pdf) - 100 руб. (word)
Задача 46. Подобрать диаметр шайбы (отверстия) в ответвлении воздухопровода для обеспечения в нем скорости v = 6 м/с при длине ответвления l = 20 м и диаметре D = 200 мм, если начальное манометрическое давление в магистрали Р = 80 + 0,5∙N Па.
Исходные данные: N = 16; Р = 80 + 0,5∙16 = 88 Па.
Задача 47
Цена - 250 руб. (pdf) - 300 руб. (word)
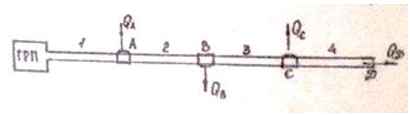
Задача 47. Определить избыточное манометрическое давление в точках А, В,С газопровода низкого давления и давление городского распределительного пункта (ГРП), если расходы QА = 100 + 2∙N = м3/час; QВ = 0,8QА; QС = 0,7QА; QD = 0,5QА, а избыточное давление в точке D РD = 100 + 0,5∙N, кПа. Трубы стальные, не новые. l1 = 100 м; d1 = 125 мм; l2 = 300 м; d2 = 200 мм; l3 = 150 м; d3 = 150 мм; l4 = 250 м; d4 = 100 мм; Коэффициент вязкости газа ν = 12·10-6 м2/с.
Исходные данные: N = 16; QА = 100 + 2∙16 = 132 м3/час; РD = 100 + 0,5∙16 = 108 кПа.
Задача 48
Цена - 150 руб. (pdf) - 180 руб. (word)
Задача 48. Определить какое давление должна создавать компрессорная станция магистрального газопровода длиной L = 100 км, диаметром d = 1,4 м для перекачки в час Qн = (1 + 0,05∙N)·106 = нм3/час природного газа с плотностью в нормальных условиях ρн = 0,73 кг/м3, вязкость газа ν = 0,143·10-4 м2/с, в конце трубопровода должно поддерживаться давление Р = 2 атм. Принять Т = 293 К, и R = 420 Дж/(кг·К).
Исходные данные: N = 16; Qн = (1 + 0,05∙16)·106 = 1,8·106 м3/час; Р = 2 атм = 202650 Па.
VI. Гидравлический расчет трубопроводов (Задачи 49-53).
Задача 49
Цена - 80 руб. (pdf) - 100 руб. (word)
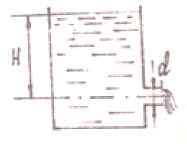
Задача 49. Определить расход воды, вытекающей через внешний цилиндрический насадок, если его диаметр d = 5 см и напор Н = 1 + 0,1N м. Движение установившееся. Какой расход будет без насадка, т.е. через отверстие?
Исходные данные: N = 16; Н = 1 + 0,1·16 = 2,6 м.
Задача 50
Цена - 80 руб. (pdf) - 100 руб. (word)
Задача 50. В водопроводе, находящемся под давлением Р = 5 + 0,1·N атм в результате сквозного проржавления образовалось отверстие диаметром d = 2 мм. Определить утечку воды за сутки.
Исходные данные: N = 16; Р = 5 + 0,1·16 = 6,6 атм.
Задача 51
Цена - 150 руб. (pdf) - 180 руб. (word)
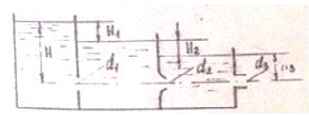
Задача 51. Определить расход через систему, включающую в себя отверстие в тонкой стенке диаметром d1 = 100 мм, коноидальный и внешний цилиндрический насадки с диаметрами d2 = 50 мм и d3 = 75 мм. Найти напоры Н1, Н2 и Н3, если полный напор Н = 1,5 + 0,1N м.
Исходные данные: N = 16; Н = 1,5 + 0,1·16 = 3,1 м.
Задача 52
Цена - 80 руб. (pdf) - 100 руб. (word)
Задача 52. Определить скорость истечения и расход природного газа через предохранительный клапан, установленный на выхлопном устройстве ГРП. Избыточное давление в системе Р = 300 + 5·N кПа, температура t = 20 °C, рабочее сечение клапана w = 20 см2, k = 1,3. Определить температуру газа в вытекающей струе.
Исходные данные: N = 16; Р = 300 + 5·16 = 380 кПа.
Задача 53
Цена - 80 руб. (pdf) - 100 руб. (word)
Задача 53. Воздух в резервуаре находится под избыточным давлением Р1 = N кПа при температуре t = 20 °C. Определить расход и скорость истечения в атмосферу через отверстие d = 0,1 м.
Исходные данные: N = 16; Р1 = 16 кПа.
VII. Гидравлический удар, струи, моделирование (Задачи 54-57).
Задача 54
Цена - 100 руб. (pdf) - 130 руб. (word)
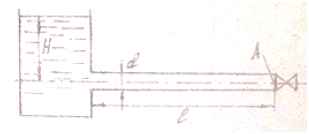
Задача 54. По стальной трубе диаметром d = 100 мм и длиной l = 100 м вытекает вода под напором Н = 5 + 0,1N м. В конце трубы расположена задвижка Определить максимальное давление перед задвижкой в случае мгновенного ее закрытия. Каким будет давление в точке А через t = 0,3 с после закрытия задвижки? Потерями на трение пренебречь. Толщину стенок принять δ = 2 мм.
Исходные данные: N = 16; Н = 5 + 0,1·16 = 6,6 м.
Задача 55
Цена - 80 руб. (pdf) - 100 руб. (word)
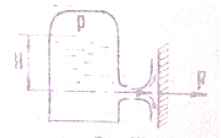
Задача 55. Определить силу давления F струи воды, вытекающей через коноидальный насадок диаметром d0 = 0,05 м под действием давления Р = 1 + 0,1N атм и напора Н = 5 + 0,05N м на вертикальную неподвижную плоскую стенку.
Исходные данные: N = 16; Н = 5 + 0,05·16 = 5,8 м ; Р = 1 + 0,1·16 = 1,6 атм.
Задача 56
Цена - 80 руб. (pdf) - 100 руб. (word)
Задача 56. Для изучения движения газов в дымоходе парового котла устроена водяная модель в масштабе 1:25. Определить необходимую скорость воды в модели, если скорость газов V2 = 10 + 0,2N м/с, температура газов t2 = 800 °C, кинематический коэффициент вязкости газа при этой температуре ν2 = 1,3 см2/с. Температура воды на модели t1 = 10 + 0,2N °C.
Исходные данные: N = 16; V2 = 10 + 0,2·16 = 13,2 м/с; t1 = 10 + 0,2·16 = 13,2 °C
Задача 57
Цена - 80 руб. (pdf) - 100 руб. (word)
Задача 57. Промывка горизонтального котла диаметром d2 = 1,65 м и длиной l2 = 10,5 м производится водой при температуре t2 = 60 °C и расходом Q2 = 60 + 0,5N л/с. Для изучения этого процесса устроена модель в масштабе 1:20. Каков должен быть расход на модели, если для моделирования используется вода с температурой t2 = 20 °C?
Исходные данные: N = 16; Q2 = 60 + 0,5·16 = 68 л/с.

