
Решение задач по ГИДРОМЕХАНИКЕ НГТУ Нижний Новгород
Сборник заданий для курсовых работ 1999 г.
В.Ф. Чеботаев, А.Б. Ваганов, П.Н. Егоров, А.В. Запорожцев,
И.Д. Краснокутский, А.Н. Попов, М.Е.Рабинович, В.Н. Савинов.

ГЛАВА 3.
КИНЕМАТИКА ЖИДКОСТИ
Задача 3.2
Задача 3.2
Цена - 100 руб. (pdf) - 120 руб. (word)
Исследовать поток с проекциями скоростей vх и vу (табл. 3.1). Построить семейство линий тока, вычислить расход жидкости через отрезок АВ и циркуляцию скорости по окружности радиусом R с центром в точке С. Исходные данные: 𝑣х = −2𝑥/(𝑥2 + 𝑦2); 𝑣𝑦 = 2𝑦/(𝑥2 + 𝑦2); 𝐴(𝑥𝐴,𝑦𝐴) = 0,5;1; 𝐵(𝑥𝐵,𝑦𝐵) = 2;4; 𝑅 = 5; 𝐶(𝑥0,𝑦0) = 2;6
Решение (pdf) Решение (docx)Задача 3.6
Цена - 100 руб. (pdf) - 120 руб. (word)
Исследовать поток с проекциями скоростей vх и vу (табл. 3.1). Построить семейство линий тока, вычислить расход жидкости через отрезок АВ и циркуляцию скорости по окружности радиусом R с центром в точке С. Исходные данные: 𝑣х = 2𝑥 + 𝑦; 𝑣𝑦 = 𝑥 − 2𝑦; 𝐴(𝑥𝐴,𝑦𝐴) = 1;1; 𝐵(𝑥𝐵,𝑦𝐵) = 2;2; 𝑅 = 2; 𝐶(𝑥0,𝑦0) = 2;2
Решение (pdf) Решение (docx)Задача 3.8
Цена - 100 руб. (pdf) - 120 руб. (word)
Исследовать поток, заданный потенциалом скорости φ (табл. 3.2). Построить линии тока. Вычислить скорости жидких частиц в точках А и В, расход через отрезок прямой, соединяющий эти точки, и циркуляцию скорости по замкнутому контуру АВС. Исходные данные: 𝜑 = 𝑥2 − 𝑦2; 𝐴(𝑥𝐴,𝑦𝐴) = 5;1; 𝐵(𝑥𝐵,𝑦𝐵) = 5;2; 𝐶(𝑥0,𝑦0) = 0;0
Решение (pdf) Решение (docx)Задача 3.14
Цена - 100 руб. (pdf) - 120 руб. (word)
Исследовать поток с функцией тока Ψ (табл. 3.3). Построить семейство линий тока. Найти уравнения линий тока, проходящих через точки А и В, расход жидкости через отрезок прямой АВ, а также циркуляцию скорости по замкнутому контуру АВС. Исходные данные: Ψ = 3(𝑥2 − 𝑦2); 𝐴(𝑥𝐴,𝑦𝐴) = 3;6; 𝐵(𝑥𝐵,𝑦𝐵) = 5;10; 𝐶(𝑥0,𝑦0) = 6;1
Решение (pdf) Решение (docx)Задача 3.18
Цена - 100 руб. (pdf) - 120 руб. (word)
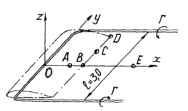
Крыло конечного удлинения заменено П - образным вихрем, лежащим в плоскости хОу (рис. 3.18). Интенсивность вихря Г. Свободные концы вихря простираются в бесконечность. Вычислить вызванные скорости в указанных точках плоскости хОу (табл. 3.4).
Решение (pdf) Решение (docx)Задача 3.25
Цена - 100 руб. (pdf) - 120 руб. (word)
Течение, полученное от сложения поступательного потока и потока источника, имеет характеристическую функцию w (табл. 3.5). Построить семейство линий тока, найти положение критической точки, составить уравнение линии тока, проходящей через критическую точку. Определить расход жидкости через отрезок АВ. Исходные данные: 𝑤 = 𝑖2𝑧 + 1,5ln(𝑧 − 𝑖);𝐴(𝑥𝐴,𝑦𝐴) = 1;5; 𝐵(𝑥𝐵,𝑦𝐵) = −1;6
Решение (pdf) Решение (docx)Задача 3.34
Цена - 100 руб. (pdf) - 120 руб. (word)
Течение вокруг кругового цилиндра задано характеристической функцией w (табл. 3.7). Построить линию тока, проходящую через точку z = 2. Вычислить расход жидкости через окружность радиусом R с центром в начале координат и циркуляцию скорости по этой окружности. Исходные данные: R = 3 м; 𝑤 = −𝑖3𝑙𝑛(𝑧 − 4)/(𝑧 − 1)
Решение (pdf) Решение (docx)
ГЛАВА 4.
ДИНАМИКА НЕВЯЗКОЙ ЖИДКОСТИ
Задача 4.7
Задача 4.7
Цена - 100 руб. (pdf) - 120 руб. (word)
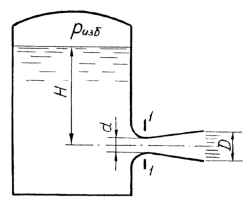
Вода вытекает из бака через диффузор в атмосферу. Пренебрегая потерями, определить, при каком избыточном давлении над свободной поверхностью воды в баке давление в узком сечении 1-1 диффузора станет теоретически равным нулю, если d : D = 0,85, а уровень H постоянен? Исходные данные: Н = 5,2 м.
Решение (pdf) Решение (docx)Задача 4.8
Цена - 100 руб. (pdf) - 120 руб. (word)

Вода вытекает из бака через диффузор в атмосферу. Пренебрегая потерями, определить, при каком избыточном давлении над свободной поверхностью воды в баке давление в узком сечении 1-1 диффузора станет теоретически равным нулю, если d : D = 0,85, а уровень H постоянен? Исходные данные: Н = 4,6 м.
Решение (pdf) Решение (docx)Задача 4.11
Цена - 100 руб. (pdf) - 120 руб. (word)
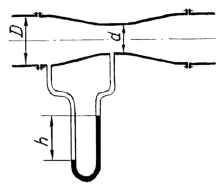
Дифференциальный ртутный манометр, присоединенный к установленной горизонтально расходомерной трубе, показывает разницу уровней h. Определить расход воды по трубе, считая ее невязкой, если диаметры расходомерной трубы D и d. Исходные данные: D = 250 мм; d = 100 мм; h = 700 мм.
Решение (pdf) Решение (docx)Задача 4.20
Цена - 100 руб. (pdf) - 120 руб. (word)
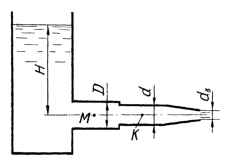
Из открытого резервуара по трубе переменного сечения вытекает вода под постоянным напором H. Пренебрегая потерями, определить расход воды, если диаметр второго участка трубы d, а d3 = 40 мм. Найти давление в точке K, расположенной на оси второго участка трубы. Исходные данные: d = 80 мм; Н = 2,4 м.
Решение (pdf) Решение (docx)Задача 4.21
Цена - 100 руб. (pdf) - 120 руб. (word)
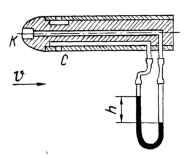
Для измерения скорости воздушного потока (ρ = 1,26 кг/м3) использована скоростная трубка с двумя отверстиями – динамическим, расположенным в критической точке K, и статическим − в точке C, где коэффициент давления равен нулю. Определить скорость воздушного потока, если показание дифференциального манометра, присоединенного к ним и залитого водой, равно h. Воздух рассматривать как невязкую жидкость. Исходные данные: h = 100 мм.
Решение (pdf) Решение (docx)Задача 4.23
Цена - 100 руб. (pdf) - 120 руб. (word)

Для измерения скорости воздушного потока использована скоростная трубка с двумя отверстиями – динамическим, расположенным в критической точке K, и статическим − в точке C, где коэффициент давления равен нулю. Определить показание дифференциального манометра, присоединенного к ним и залитого ртутью (ρрт = 13,6∙103 кг/м3), если скорость самолета составляет 720 км/ч. Воздух считать невязкой жидкостью с плотностью ρ = 1,22 кг.
Решение (pdf) Решение (docx)Задача 4.33
Цена - 100 руб. (pdf) - 120 руб. (word)
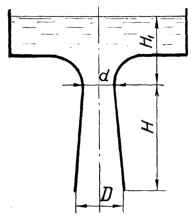
Керосин (ρ = 810 кг/м3) вытекает из резервуара по расширяющейся трубе – диффузору в атмосферу. Уровень жидкости в резервуаре Н1 = 0,8 м. Считая жидкость невязкой, определить давление в узком сечении диффузора, если его размеры D, d, H заданы. Исходные данные: D = 120 мм; d = 90 мм; H = 1,2 м;
Решение (pdf) Решение (docx)Задача 4.42
Цена - 100 руб. (pdf) - 120 руб. (word)
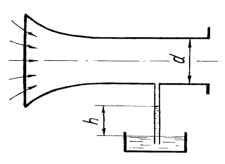
Центробежный вентилятор засасывает воздух из атмосферы через трубу. К цилиндрической части трубы, диаметр которой d, присоединена стеклянная трубка, нижним концом опущенная в сосуд с водой. Определить расход засасываемого воздуха (ρ = 1,24 кг/м3), если вода в трубке поднялась на высоту h. Исходные данные: d = 180 мм; h = 120 мм.
Решение (pdf) Решение (docx)
ГЛАВА 5.
ИСТЕЧЕНИЕ ЖИДКОСТИ ЧЕРЕЗ ОТВЕРСТИЯ, НАСАДКИ И ГИДРОАППАРАТЫ
Задача 5.5
Задача 5.5
Цена - 100 руб. (pdf) - 120 руб. (word)
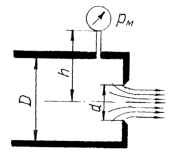
Определить расход воды Q через отверстие с острой кромкой диаметром d, выполненное в торце трубы диаметром D, если показание манометра перед отверстием pм и высота расположения манометра над осью трубы h. Как изменится расход, если к отверстию присоединить цилиндрический насадок? Давление на выходе из насадка атмосферное. Исходные данные: D = 200 мм; d = 120 мм; h = 1,3 м; pм = 0,1 МПа;
Решение (pdf) Решение (docx)Задача 5.10
Цена - 100 руб. (pdf) - 120 руб. (word)
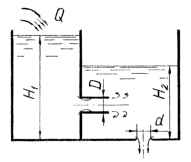
В бак, разделенный перегородкой на два отсека, подается керосин в количестве Q = 4,0 л/с. В перегородке имеется цилиндрический насадок, диаметр которого D. Керосин из второго отсека через отверстие диаметром d вытекает наружу, в атмосферу. Определить высоты H1 и H2 уровней керосина, считая их постоянными. Исходные данные: D = 60 мм; d = 40 мм;
Решение (pdf) Решение (docx)Задача 5.11
Цена - 100 руб. (pdf) - 120 руб. (word)
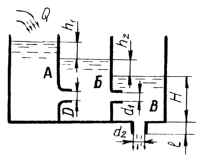
В резервуар А подается вода, откуда через сопло диаметром D перетекает в резервуар Б. Далее через цилиндрические насадки вода попадает в резервуар В и, наконец, вытекает в атмосферу. Диаметры насадок соответственно d1 =10 мм и d2 = 6 мм, а длина l = 25 мм. Высота уровня воды в резервуаре В равна Н. Определить расход воды через систему и перепады уровней h1 и h2, предполагая режим установившимся. Коэффициент расхода сопла принять μ = 0,97. Исходные данные: D = 8 мм; Н = 1,1 м;
Решение (pdf) Решение (docx)Задача 5.12
Цена - 100 руб. (pdf) - 120 руб. (word)

В резервуар А подается вода, откуда через сопло диаметром D перетекает в резервуар Б. Далее через цилиндрические насадки вода попадает в резервуар В и, наконец, вытекает в атмосферу. Диаметры насадок соответственно d1 =10 мм и d2 = 6 мм, а длина l = 25 мм. Высота уровня воды в резервуаре В равна Н. Определить расход воды через систему и перепады уровней h1 и h2, предполагая режим установившимся. Коэффициент расхода сопла принять μ = 0,97.Исходные данные: D = 10 мм; Н = 1,4 м;
Решение (pdf) Решение (docx)Задача 5.20
Цена - 100 руб. (pdf) - 120 руб. (word)
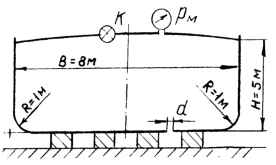
Отсек судна с сечением, изображенном на рисунке, длиной L = 10,0 м при гидравлических испытаниях заполнен водой под давлением pм. Определить время опорожнения отсека через донное отверстие диаметром d, если одновременно будет открыт обратный клапан К. Как изменится время опорожнения, если над поверхностью воды в отсеке поддерживать постоянное избыточное давление pм? Исходные данные: Н = 4,6 м; d = 90 мм; pм = 0,08 МПа.
Решение (pdf) Решение (docx)Задача 5.21
Цена - 100 руб. (pdf) - 120 руб. (word)
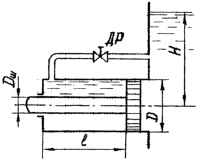
Гидравлическое реле времени состоит из цилиндра, в котором помещен поршень со штоком-толкателем. Диаметр поршня − D, а штока – Dш. Цилиндр присоединен к емкости с постоянным уровнем Н жидкости. Под действием давления, передающегося из емкости в правую полость цилиндра, поршень перемещается, вытесняя жидкость из левой полости в ту же емкость через трубку и дроссель с площадью проходного сечения S0 = 25 мм2. Вычислить время срабатывания реле, определяемое перемещением поршня на расстояние l = 100 мм из начального положения до упора в торец цилиндра. Коэффициент расхода дросселя принять μ = 0,65. Потерями в трубке, кроме потерь напора на дросселе, пренебречь. Исходные данные: D = 80 мм; Н = 0,9 м; Dш = 40 мм.
Решение (pdf) Решение (docx)Задача 5.25
Цена - 100 руб. (pdf) - 120 руб. (word)
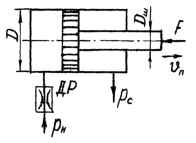
Определить скорость поршня гидроцилиндра при движении против нагрузки F. Давление на входе в дроссель ДР pн, на сливе pс = 0,30 МПа. Диаметры: поршня D, штока Dш, отверстия дросселя d. Коэффициент расхода дросселя принять μ = 0,62. Рабочая жидкость – масло (ρ = 900 кг / м3). Исходные данные: D = 70 мм; d = 1,2 мм; pн = 20 МПа; Dш = 30 мм; F = 55 кН.
Решение (pdf) Решение (docx)Задача 5.39
Цена - 100 руб. (pdf) - 120 руб. (word)
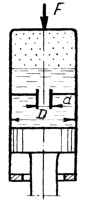
На рисунке показана упрощенная схема самолетного гидропневмоамортизатора. Процесс амортизации при посадке самолета происходит за счет проталкивания рабочей жидкости (ρ = 900 кг/м3) через отверстие диаметром d (коэффициент расхода μ = 0,75) и за счет сжатия воздуха. Диаметр поршня D. Определить скорость движения цилиндра относительно поршня в начальный момент амортизации, когда давление воздуха в верхней части амортизатора p, расчетное усилие F. Исходные данные: D = 100 мм; d = 8 мм; p = 0,2 МПа; F = 50 кН.
Решение (pdf) Решение (docx)
ГЛАВА 6.
ГИДРАВЛИЧЕСКИЙ РАСЧЕТ ТРУБОПРОВОДОВ
Задача 6.2
Задача 6.2
Цена - 100 руб. (pdf) - 120 руб. (word)
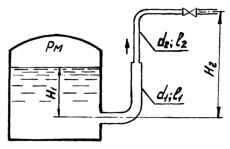
Из резервуара по трубопроводу (d1, l1 и d2, l2) подается вода на высоту H2 = 12,0 м. Шероховатость стенок трубопровода Δ = 0,15 мм. Коэффициент сопротивления для поворотов принять равным ζпов = 0,3, а для крана − ζк. Какое давление необходимо поддерживать в резервуаре, если уровень воды в нем принять постоянным, равным H1, а расход воды через кран равен Q = 1,2 л/с? Исходные данные: d1 = 22 мм; l1 = 10 м; d2 = 35 мм; l2 = 15 м; H1 = 1,6 м; ζк = 5,0; ν = 0,013 Ст.
Решение (pdf) Решение (docx)Задача 6.13
Цена - 100 руб. (pdf) - 120 руб. (word)
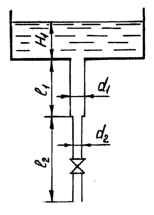
Из открытого резервуара через вертикальную трубу (d1, l1 и d2, l2) в атмосферу вытекает вода. Уровень в резервуаре постоянный, глубина H1. Шероховатость стенок труб Δ = 0,35 мм. Коэффициент сопротивления крана ζк. Определить расход воды. Исходные данные: d1 = 60 мм; l1 = 1 м; d2 = 40 мм; l2 = 1,8 м; H1 = 0,8 м; ζк = 6; ν = 0,013 Ст.
Решение (pdf) Решение (docx)Задача 6.22
Цена - 100 руб. (pdf) - 120 руб. (word)
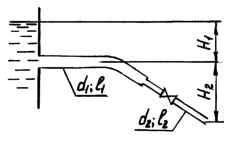
Вода вытекает в атмосферу из резервуара с постоянным уровнем по трубопроводу (d1, l1 и d2, l2). Горизонтальный участок заглублен под уровень на H1, наклонный участок имеет высоту H2 = 15,0 м. Шероховатость стенок трубопровода Δ = 0,20 мм, потерю напора на повороте не учитывать. Определить, каков должен быть коэффициент сопротивления задвижки ζ при расходе в трубопроводе Q = 17 л/с? Исходные данные: d1 = 80 мм; l1 = 50 м; d2 = 90 мм; l2 = 40 м; H1 = 3 м; ν = 0,015 Ст.
Решение (pdf) Решение (docx)Задача 6.23
Цена - 100 руб. (pdf) - 120 руб. (word)

Вода вытекает в атмосферу из резервуара с постоянным уровнем по трубопроводу (d1, l1 и d2, l2). Горизонтальный участок заглублен под уровень на H1, наклонный участок имеет высоту H2 = 15,0 м. Шероховатость стенок трубопровода Δ = 0,20 мм, коэффициент сопротивления вентиля ζв, поворота − ζпов = 0,25. Определить расход воды. Исходные данные: d1 = 100 мм; l1 = 50 м; d2 = 80 мм; l2 = 50 м; H1 = 2,4 м; ζв = 7; ν = 0,011 Ст.
Решение (pdf) Решение (docx)Задача 6.32
Цена - 100 руб. (pdf) - 120 руб. (word)
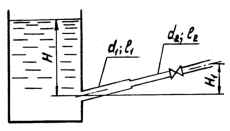
Из открытого резервуара по трубопроводу (d1, l1 и d2, l2) происходит истечение воды в атмосферу. Выходное отверстие расположено выше входного на величину H1. Шероховатость стенок трубопровода Δ = 0,50 мм, коэффициент сопротивления крана ζк. Определить, при каком напоре Н можно получить расход Q = 5,6 л/с? Исходные данные: d1 = 60 мм; l1 = 12 м; d2 = 80 мм; l2 = 15 м; H1 = 1,4 м; ζк = 5,5; ν = 0,015 Ст.
Решение (pdf) Решение (docx)Задача 6.45
Цена - 100 руб. (pdf) - 120 руб. (word)
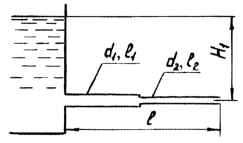
Для подачи воды в количестве Q = 0,025 м3/с на расстояние l = 500 м под напором H1 можно использовать трубы диаметром d1 и d2, шероховатость стенок которых Δ = 1,0 мм. Определить необходимые длины участков l1 и l2. Исходные данные: d1 = 200 мм; d2 = 150 мм; Н1 = 6 м; ν = 0,013 Ст.
Решение (pdf) Решение (docx)Задача 6.46
Цена - 100 руб. (pdf) - 120 руб. (word)

Для подачи воды в количестве Q = 0,025 м3/с на расстояние l = 500 м под напором H1 можно использовать трубы диаметром d1 и d2, шероховатость стенок которых Δ = 1,0 мм. Определить необходимые длины участков l1 и l2. Исходные данные: d1 = 150 мм; d2 = 200 мм; Н1 = 8 м; ν = 0,01 Ст.
Решение (pdf) Решение (docx)Задача 6.50
Цена - 100 руб. (pdf) - 120 руб. (word)
По горизонтальному трубопроводу длиной l1 необходимо перекачивать нефть (ρ = 910 кг/м3) с расходом Q = 60 л/с при условии, чтобы падение давления в трубопроводе не превышало Δр = 4,0 МПа. Шероховатость стенок трубопровода Δ = 0,20 мм. Определить диаметр трубопровода. Исходные данные: l1 = 12000 м; ν = 0,4 Ст.
Решение (pdf) Решение (docx)
ГЛАВА 7.
ПРИМЕНЕНИЕ ЗАКОНОВ КОЛИЧЕСТВА ДВИЖЕНИЯ И МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ К ЖИДКОСТЯМ
Задача 7.10
Задача 7.10
Цена - 100 руб. (pdf) - 120 руб. (word)
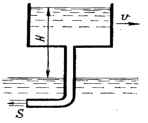
Определить реакцию и полезную механическую мощность, развиваемую потоком воды на подвижном сосуде, который перемещается со скоростью v и из которого жидкость вытекает через трубу с выходным сечением S = 25 см2 под постоянным напором H. Гидравлическими сопротивлениями пренебречь. Исходные данные: v = 5 м/c; Н = 5 м.
Решение (pdf) Решение (docx)Задача 7.13
Цена - 100 руб. (pdf) - 120 руб. (word)
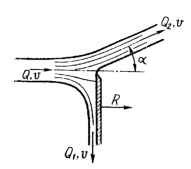
Пластина, введенная в свободную струю воды перпендикулярно ее оси, отсекает часть расхода струи Q1 и вызывает отклонение остальной части струи на угол α. Определить силу воздействия струи на пластину и угол отклонения α, если скорость струи v, полный расход Q = 36 л/с. Весомостью жидкости и трением струи о пластину пренебречь. Исходные данные: v = 30 м/с; Q1 = 12 л/с;
Решение (pdf) Решение (docx)Задача 7.30
Цена - 100 руб. (pdf) - 120 руб. (word)
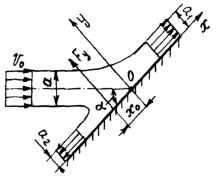
Найти общее выражение величины и точку приложения равнодействующей избыточного гидродинамического давления на единицу ширины при косом ударе плоской струи о неподвижную плоскость и вычислить их значение для воды при a = 0,1 м, v0 = v и угле α. Потерями энергии при течении жидкости вдоль плоскости пренебречь, профили скорости в удаленных сечениях струи считать равномерными. Исходные данные: v = 10 м/с; α = 30 °.
Решение (pdf) Решение (docx)Задача 7.31
Цена - 100 руб. (pdf) - 120 руб. (word)
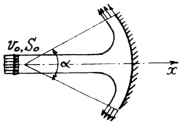
Найти общее выражение силы избыточного гидродинамического давления, вызываемой струей воды, направленной вдоль оси симметрии на неподвижную криволинейную поверхность. Вычислить ее значение при S0 = 0,06 м2 и угле α, потерями энергии вдоль струи пренебречь, профили скорости в удаленных сечениях струи считать равномерными. Исходные данные: v0 = 12 м/c; α = 120°.
Решение (pdf) Решение (docx)Задача 7.39
Цена - 100 руб. (pdf) - 120 руб. (word)
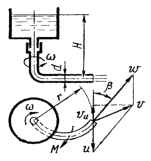
Вода вытекает из резервуара через изогнутую вращающуюся трубку при постоянном напоре Н. Диаметр трубки d = 40 мм, выходной радиус r = 0,5 м, выходной угол β. Коэффициент потерь при течении воды по трубке ζ = 0,2. Определить момент действия потока на трубку при равномерном вращении с угловой скоростью ω = 5 1/с. При какой скорости вращения момент действия потока на трубку станет равным нулю? Исходные данные: Н = 2 м; β = 30°.
Решение (pdf) Решение (docx)Задача 7.41
Цена - 100 руб. (pdf) - 120 руб. (word)
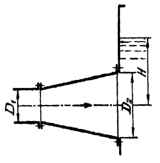
Из диффузора, входной и выходной диаметры которого D1 = 250 мм, D2 = 500 мм, вода поступает в бак с постоянным уровнем Н со скоростью v2 = v. Определить осевую силу, действующую на диффузор при коэффициенте потерь в ζ = 0,25. При каком вакууме в баке искомая сила будет равна нулю? Указания. Потери в диффузоре hп.д = ζ(v1 - v2)2/2g. Вакуум рв вычитается из избыточных давлений в сечениях. Исходные данные: v = 2 м/с; H = 4 м;
Решение (pdf) Решение (docx)Задача 7.42
Цена - 100 руб. (pdf) - 120 руб. (word)

Из диффузора, входной и выходной диаметры которого D1 = 250 мм, D2 = 500 мм, вода поступает в бак с постоянным уровнем Н со скоростью v2 = v. Определить осевую силу, действующую на диффузор при коэффициенте потерь в ζ = 0,25. При каком вакууме в баке искомая сила будет равна нулю? Указания. Потери в диффузоре hп.д = ζ(v1 - v2)2/2g. Вакуум рв вычитается из избыточных давлений в сечениях. Исходные данные: v = 2,2 м/с; H = 3 м;
Решение (pdf) Решение (docx)Задача 7.46
Цена - 100 руб. (pdf) - 120 руб. (word)
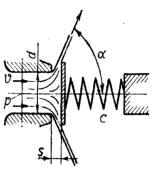
Предохранительный клапан с седлом диаметром d = 24 мм пропускает при избыточном давлении в седле p = 3,0 МПа расход масла (ρ = 910 кг/м3), равный Q, при этом открытие клапана S = 5 мм. Считая жидкость невязкой, рассчитать жесткость пружины клапана, если известно, что начальное давление открытия клапана p0, а струя из клапанной щели должна вытекать под углом α ≥ 70°. Исходные данные: p0 = 2,6 МПа; Q = 8 л/с.
Решение (pdf) Решение (docx)
ГЛАВА 8.
ГИДРОДИНАМИЧЕСКОЕ ПОДОБИЕ
Задача 8.20
Задача 8.20
Цена - 100 руб. (pdf) - 120 руб. (word)
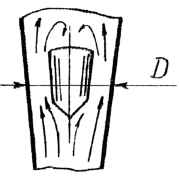
Работа ротаметра, имеющего диаметр трубки Dн и пропускающего Qн керосина (ρн = 790 кг/м3), основана на уравновешивании веса поплавка в жидкости силой действия потока. Определить: 1) расход воды (νм = 0,010 Ст) в модельном ротаметре, выполненном в масштабе KL, если зоне турбулентной автомодельности соответствует условие Re ≥ 105; 2) плотность материала поплавка модельного ротаметра, если в натурном ротаметре он сделан из алюминия (ρпн = 2700 кг/м3). Исходные данные: KL = 2; Dн = 0,05 м; Qн = 10 л/с; νн = 0,03 Ст.
Решение (pdf) Решение (docx)Задача 8.23
Цена - 100 руб. (pdf) - 120 руб. (word)
Аэродинамическое сопротивление автомобиля высотой hн = 1,4 м определяется продувкой его модели в аэродинамической трубе. Кинематический коэффициент вязкости воздуха ν = 0,156 Ст; зона автомодельности при Re ≥ 105. Определить: 1) максимальный масштаб модели KL, если скорость автомобиля vн, а скорость продувки модели vм = 45 м/с; 2) отношение сил сопротивления модели и натуры. Исходные данные: vн = 32 м/с.
Решение (pdf) Решение (docx)Задача 8.26
Цена - 100 руб. (pdf) - 120 руб. (word)
Измерительная диафрагма диаметром D и отношением d/D = 0,65 испытывается на воде (νм = 0,01 Ст). Зона турбулентной автомодельности (постоянство градуировочного коэффициента) начинается при расходе воды Qм = 11,8 л/с, при этом показание ртутного дифманометра составило hм. Определить: 1) расход Qн, соответствующий началу зоны турбулентной автомодельности, при работе диафрагмы на воздухе (ρн = 1,17 кг/м3); 2) показание водяного дифманометра при работе диафрагмы на воздухе. Исходные данные: KL = 1; Dн = 0,12 м; hм = 0,073 м; νн = 0,146 Ст.
Решение (pdf) Решение (docx)Задача 8.31
Цена - 100 руб. (pdf) - 120 руб. (word)
Истечение нефти через насадок диаметром Dн при малом напоре Hн = 2,5Dн исследуется на модели, работающей на воде (νм = 0,01 Ст). Определить: 1) диаметр модельного насадка Dм; 2) расход через натурный насадок Qн, если на модели получен расход воды Qм = 0,056 м3/с. Исходные данные: Dн = 0,1 м; Qн = 0,056 м3/с; νн = 0,25 Ст.
Решение (pdf) Решение (docx)Задача 8.35
Цена - 100 руб. (pdf) - 120 руб. (word)
Определить скорость буксировки модели надводного судна если модель выполнена в масштабе KL. Длина натурного судна Lн = 100 м, а его скорость υн. Модель испытывается в зоне турбулентной автомодельности – при температуре 15 °С (νм = 0,0114 Ст). Вычислить также числа Фруда и Рейнольдса для натуры и модели. Исходные данные: KL = 16 м; vн = 10,5 м/с; νн = 0,0157 Ст.
Решение (pdf) Решение (docx)Задача 8.40
Цена - 100 руб. (pdf) - 120 руб. (word)
Модель надводного судна с работающими гребными винтами, выполненная в масштабе KL, испытывается в бассейне. Предполагая, что при испытаниях обеспечено гидродинамическое подобие в зоне турбулентной автомодельности, определить: 1) скорость буксировки модели, если скорость движения натурного судна vн; 2) масштаб сил Fн:Fм, действующих на корпус судна, считая плотность воды в натурных и модельных условиях одинаковой; 3) масштаб буксировочной мощности Nн:Nм. Исходные данные: KL = 20; vн = 16 м/с.
Решение (pdf) Решение (docx)Задача 8.42
Цена - 100 руб. (pdf) - 120 руб. (word)
Для проведения буксировочных испытаний модели озерного теплохода длиной Lн = 62 м и объемным водоизмещением Vн = 635 м3 необходимо установить масштаб, массу и скорость буксировки модели при обеспечении гидродинамического подобия, если скорость движения натуры vн, а начало зоны турбулентной автомодельности соответствует Re = 2 ∙ 106. Температура воды при модельных испытаниях t = 20 °С (νм = 0,010 Ст). Исходные данные: vн = 6,4 м/с.
Решение (pdf) Решение (docx)Задача 8.44
Цена - 100 руб. (pdf) - 120 руб. (word)
Модель подводного судна, имеющего длину Lн = 30 м, изготовлена в масштабе KL. Скорость натурного судна vн. Определить скорость буксировки модели при испытаниях в бассейне и скорость продувки модели в аэродинамической трубе. Кинематический коэффициент вязкости воды при модельных испытаниях νмв = 0,0114 Ст, воздуха νмвз = 0,146 Ст. Исходные данные: KL = 12; vн = 6 м/с; νн = 0,0157 Ст.
Решение (pdf) Решение (docx)Задача 8.50
Цена - 100 руб. (pdf) - 120 руб. (word)
Модель судового гребного винта изготовлена в масштабе KL. Испытания в бассейне проводятся по условиям подобия сил тяжести при температуре воды 20 °С (νм = 0,010 Ст). Определить число оборотов модели nм, если для натурного гребного винта nн = 10 об/с, его диаметр Dн. Скорость натурного судна vн. Вычислить значения Reн и Reм. Исходные данные: KL = 5; Dн = 2 м; vн = 12,5 м/с, νн = 0,0157 Ст.
Решение (pdf) Решение (docx)
ГЛАВА 9.
РАБОТА НАСОСОВ НА СЕТЬ
Задача 9.11
Задача 9.11
Цена - 150 руб. (pdf) - 180 руб. (word)
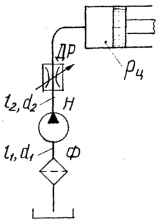
Шестеренный насос подает масло (турбинное 30) из открытого гидробака в полость гидроцилиндра, где избыточное давление pц = 2,40 МПа. Температура перекачиваемого масла T. Линии всасывания и нагнетания, выполненные из алюминиевых труб, соответственно имеют диаметр d1 и d2 , длину l1 и l2. На линии всасывания имеется фильтр с коэффициентом сопротивления ζф = 5. Определить давление и подачу насоса для двух случаев перекрытия дросселя, установленного на линии нагнетания: коэффициент его сопротивления ζдр = 9 и ζдр = 200. Местными сопротивлениями, кроме фильтра и дросселя, пренебречь. Характеристика насоса с клапаном Qн = f (pн ) задана: Qн, л/с 0,00 0,52 0,60 pн, МПа 3,5 3,2 0,00. Исходные данные: l1 = 0,8 м; d1 = 16 мм; l2 = 4,6 м; d2 = 12 мм; t = 40 ℃.
Решение (pdf) Решение (docx)Задача 9.26
Цена - 150 руб. (pdf) - 180 руб. (word)
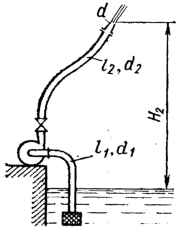
Определить подачу и мощность центробежного пожарного насоса при n = 3000 об/мин, если насос подает воду по шлангам размерами l1, d1 (λ1 = 0,025; ζ1 = 4) и l2, d2 (λ2 = 0,035; ζ2 = 10) через сходящийся насадок диаметром d = 40 мм (ζ = 0,08 ) на высоту H2. Как изменятся подача и напор насоса, если частота вращения рабочего колеса уменьшится на 15 %? Исходные данные: Н2 = 20 м; l1 = 5 м; d1 = 90 мм; l2 = 36 м; d2 = 80 мм;
Решение (pdf) Решение (docx)Задача 9.32
Цена - 150 руб. (pdf) - 180 руб. (word)
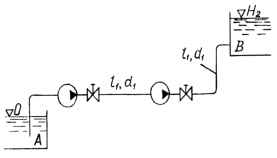
Два последовательно соединенных одинаковых центробежных насоса перекачивают воду при n1 = n2 = 1000 об/мин. из водохранилища А с отметкой уровня ∇ = 0 в бассейн В с отметкой уровня ∇ = H2 по стальному трубопроводу общей длиной l1 и диаметром d1. Суммарный коэффициент местных сопротивлений ζ = 12. Температура воды Т. Определить подачу насосов и потребляемую каждым из них мощность. Как необходимо изменить частоту вращения одного из насосов, чтобы увеличить расход в трубопроводе на 25 %? Исходные данные: Н2 = 25 м; l1 = 800 м; d1 = 200 мм; T = 15 ℃.
Решение (pdf) Решение (docx)Задача 9.34
Цена - 150 руб. (pdf) - 180 руб. (word)
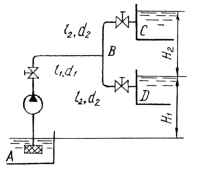
Центробежный насос, работая при n = 1450 об/мин, подает воду из резервуара А в баки С и D. Расстояния между уровнями в резервуаре и баках H1 = 25,0 м и H2. Система трубопроводов состоит из трубы АВ размерами d1 и l1 и двух одинаковых ветвей ВС и ВD размерами d2 и l2. Трубы стальные сварные. Местные сопротивления учтены эквивалентными длинами, включенными в заданные длины труб. Температура воды Т. Определить подачу воды в баки С и D и мощность насоса. При какой частоте вращения насоса (в случае тех же открытий вентилей) подача в бак С прекратится. Исходные данные: Н2 = 12 м; l1 = 30 м; d1 = 80 мм; l2 =16 м; d2 = 50 мм; Т = 10 ℃.
Решение (pdf) Решение (docx)Задача 9.35
Цена - 150 руб. (pdf) - 180 руб. (word)
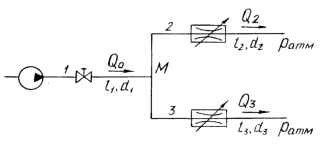
Насос обеспечивает расход Q0 по трубопроводу длиной l1 (включая линию всасывания) и диаметром d1, в котором установлен вентиль с коэффициентом сопротивления ζв = 2,0. В точке М трубопровод разветвляется на две ветви, одна из которых размерами l2 и d2 содержит дроссель с коэффициентом сопротивления ζ2 = 5,0, а другой размерами l3 = 1,2l2 и d3 = d2 − дроссель с ζ3 = 4ζ2. Трубы стальные бесшовные. Определить расходы бензина в ветвях, давление и полезную мощность насоса, если температура бензина Т. Давление в конечных сечениях труб атмосферное и геометрические высоты одинаковы. Как изменятся параметры насоса, если дроссель на линии 2 полностью закрыть? Исходные данные: Q0 = 4 л/с; l1 = 8 м; d1 = 50 мм; l2 =9 м; d2 = 40 мм; Т = 20 ℃.
Решение (pdf) Решение (docx)Задача 9.37
Цена - 150 руб. (pdf) - 180 руб. (word)
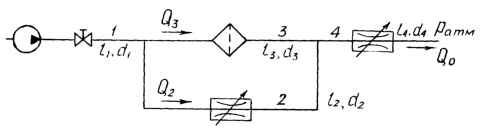
Определить давление и полезную мощность насоса, если известна его подача Q0 при работе на трубопровод размерами: l1 (включая линию всасывания) и d1, l2 и d2, l3 = 1,5l2 и d3 = d2, l4 = l1 и d4 = d1. Трубы изготовлены из латуни, перекачиваемая жидкость – масло трансформаторное при температуре Т. Коэффициенты сопротивления фильтра ζ3 = 10, дросселей ζ2 = 5 и ζ4 = 4 вентиля ζ1 = 3. В конечных сечениях труб давление атмосферное и геометрические высоты одинаковы. Как изменятся параметры насоса, если линия 3 из-за загрязненности фильтра полностью перекроется? Исходные данные: Q0 = 2,4 л/с; l1 = 2,5 м; d1 = 25 мм; l2 = 1,4 м; d2 = 20 мм; Т = 45 ℃.
Решение (pdf) Решение (docx)Задача 9.38
Цена - 150 руб. (pdf) - 180 руб. (word)

Определить давление и полезную мощность насоса, если известна его подача Q0 при работе на трубопровод размерами: l1 (включая линию всасывания) и d1, l2 и d2, l3 = 1,5l2 и d3 = d2, l4 = l1 и d4 = d1. Трубы изготовлены из латуни, перекачиваемая жидкость – масло трансформаторное при температуре Т. Коэффициенты сопротивления фильтра ζ3 = 10, дросселей ζ2 = 5 и ζ4 = 4 вентиля ζ1 = 3. В конечных сечениях труб давление атмосферное и геометрические высоты одинаковы. Как изменятся параметры насоса, если линия 3 из-за загрязненности фильтра полностью перекроется? Исходные данные: Q0 = 1,8 л/с; l1 = 2,4 м; d1 = 20 мм; l2 = 1,6 м; d2 = 16 мм; Т = 40 ℃.
Решение (pdf) Решение (docx)Задача 9.40
Цена - 150 руб. (pdf) - 180 руб. (word)
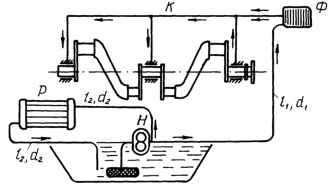
В двигателе внутреннего сгорания подача масла для смазки коренных подшипников коленчатого вала производится насосом Н по трубе размерами ℓ1, d1, фильтр Ф и распределительный канал К, от которого отходят три отводных канала размерами ℓ2, d2 к серединам подшипников. Часть подачи насоса по трубке размерами ℓ3, d3 подается в радиатор р, из которого по такой же трубке сливается в картер. Определить давление насоса и расход масла через подшипники и радиатор. Сопротивление фильтра и радиатора принять эквивалентным сопротивлению трубок длиной ℓф = 100d1 и ℓр = 1300d2, а суммарное сопротивление распределительного канала с отводными каналами и подшипниками – сопротивлению трубки длиной ℓк = 0,80 м при диаметре d = 4 мм. Свойства масла: кинематическая вязкость ν = 0,3 Ст, плотность ρ = 900 кг/м3. Давление в распределительном канале считать постоянным по длине. Характеристика насоса задана: Q, л/с 0 0,1 0,12рн, МПа 0,7 0,6 0. Исходные данные: l1 = 0,9 м; d1 = 12 мм; l2 = 1 м; d2 = 6 мм;
Решение (pdf) Решение (docx)
ГЛАВА 10.
ОБЪЕМНЫЙ ГИДРОПРИВОД
Задача 10.2
Задача 10.2
Цена - 100 руб. (pdf) - 120 руб. (word)
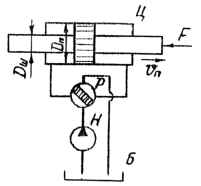
В ОГП поступательного движения используется гидроцилиндр с двухсторонним штоком. диаметры Dп, Dш = Dп/2, КПД ηоц = 0,99, ηмц = 0,96, шток нагружен силой F и движется со скоростью vп. Гидролинии выполнены из трубки диаметром d, длина общая от насоса до бака l, система заполнена жидкостью Ж, расчетная температура T. Коэффициент сопротивления распределителя ζр = 1,5. Определить подачу насоса, развиваемое им давление pн и потребляемую мощность Nпот, если КПД насоса ηн = 0,78. Исходные данные: Масло трансформаторное; F = 12 кН; vп = 0,05 м/с; d = 10 мм; Dп = 60 мм = 0,06 м; l = 8 м; Т = 10 ℃.
Решение (pdf) Решение (docx)
