Задачи по ГИДРОСТАТИКЕ АГЗ МЧС России г. Красногорск
Учебно - методическое пособие по выполнению курсовых расчетно - графических работ но курсу ГИДРОГАЗОДИНАМИКИ. Книга I и Книга II. 1999 г.
Булгаков В.И.
Кафедра физики

1. ОПРЕДЕЛЕНИЕ ДАВЛЕНИЯ В ПОКОЯЩЕЙСЯ ЖИДКОСТИ. ОСНОВНОЕ УРАВНЕНИЕ ГИДРОСТАТИКИ
1.3. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Задача 1.2
Цена - 100 руб. (pdf) - 130 руб. (word)
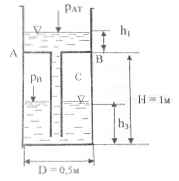
При заливке в показанный на рисунке резервуар воды, взятой в количестве G = 200 кГ, в «трюме» резервуара над жидкостью остается сжатый воздух. Требуется определить:
1) глубину h3 наполнения жидкостью нижней части резервуара;
2) давление Рв воздуха в пространстве АС;
3) равнодействующую сил давления воды и воздуха на промежуточное днище АВ.
Процесс сжатия воздуха в пространстве АС считать изотермическим.
Задача 1.5
Цена - 100 руб. (pdf) - 130 руб. (word)
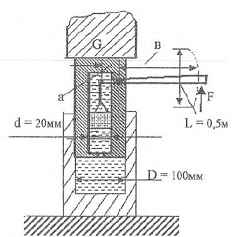
Определить :
1) усилие F , которое нужно приложить к рукоятке гидравлического домкрата для подъема груза весом G = 50000 Н;
2) перемещение h груза за один ход рукоятки.
Соотношение плеч рычага а/Ь = 1/10. КПД домкрата принять равным η = 0,8.
Задача 1.6
Цена - 100 руб. (pdf) - 130 руб. (word)
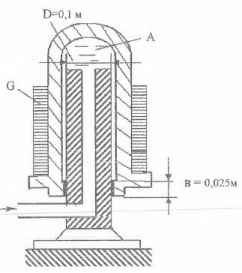
Изображенный на рисунке гидравлический аккумулятор заряжается насосом, нагнетающим воду в цилиндр А и заставляющим его подниматься вместе с грузом G = 150000 Н. При разрядке аккумулятора цилиндр опускается, и вода подается потребляющему ее агрегату. Определить:
1) давление воды при зарядке и при разрядке аккумулятора;
2) КПД аккумулятора. Коэффициент трения уплотняющей цилиндр А манжеты о плунжер f = 0,1.
Задача 1.7
Цена - 100 руб. (pdf) - 130 руб. (word)
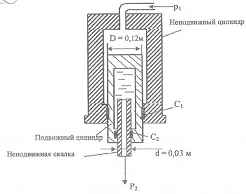
Гидравлический повыситель давления получает воду от насоса под давлением P1 = 800 кПа. Определить давление воды на выходе Р2, если вес подвижного цилиндра G = З·103 Н. Силы трения принять: в сальнике C1 - равной 1% от силы давления воды на подвижный цилиндр сверху, а в сальнике С2 - равной 3% от силы давления воды на торец скалки.
Решение (pdf) Решение (docx)Задача 1.8
Цена - 100 руб. (pdf) - 130 руб. (word)
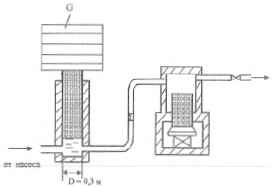
Гидравлический аккумулятор с диаметром плунжера D = 0,3 м обслуживает периодически действующий пресс с рабочим давлением Р = 5 МПа и питается непрерывно работающим насосом. Определить:
1) вес движущихся частей аккумулятора G;
2) ход S плунжера аккумулятора, учитывая, что пресс работает 1 минуту с пятиминутным перерывом, потребляя во время работы 1.9 л/с воды;
3) мощность N насоса, питающего аккумулятор водой, считая КПД насоса равным η = 0,7.
Задача 1.10
Цена - 100 руб. (pdf) - 130 руб. (word)
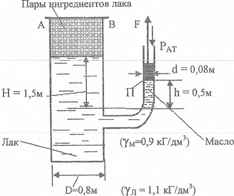
Используя приведенные на рисунке данные, определить силу, которую нужно приложить к поршеньку П, чтобы вакуум (hвак) в пространстве над лаком достиг 610 мм ртутного столба (γР.Т. = 13,6 кГ/дм3). Какова при этом будет сила суммарного давления паров ингредиентов лака и атмосферного воздуха на крышку АВ резервуара?
Решение (pdf) Решение (docx)Задача 1.11
Цена - 100 руб. (pdf) - 130 руб. (word)
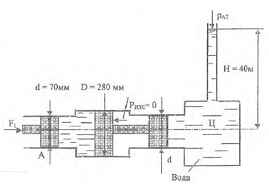
На рисунке представлена схема гидравлического бустера, обеспечивающего получение на выходе из него ( в цилиндре Ц) давления, во много раз превышающего то, которое создается под поршнем А приложенным к его штоку усилием. Определить усилие F1 которое нужно приложить к штоку поршня А, чтобы поднять воду из цилиндра Ц на высоту Н = 40 м. Считать, что сила трения каждого из трех поршней о стенки соответствующего цилиндра составляет 1/10 от силы давления жидкости (воды) на данный поршень.
Решение (pdf) Решение (docx)Задача 1.13
Цена - 100 руб. (pdf) - 130 руб. (word)
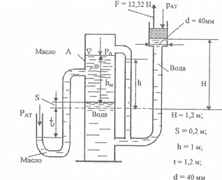
Используя приведенные на рисунке данные, определит давление РО в котле А, плотность ρм и высоту столба hM масла.
Решение (pdf) Решение (docx)Задача 1.14
Цена - 100 руб. (pdf) - 130 руб. (word)
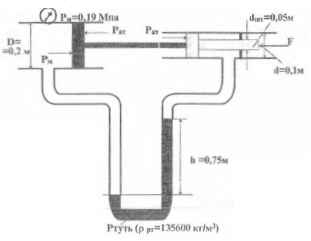
В обоих цилиндрах и в дифманометре над ртутью жидкость с плотностью ρ = 1600 кг/м3. Требуется определить усилие F, удерживающее изображенную на рисунке систему в равновесии.
Решение (pdf) Решение (docx)Задача 1.15
Цена - 100 руб. (pdf) - 130 руб. (word)
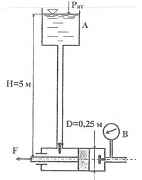
Поршневой насос перекачивает деготь (ρ = 1200 кг/м3) в резервуар А. Определить усилие F, которое нужно приложить к штоку поршня для поддержания его в равновесии. Вакуумметр показывает вакуумметрическую высоту hвак = 228 мм. рт.ст.
Решение (pdf) Решение (docx)Задача 1.16
Цена - 100 руб. (pdf) - 130 руб. (word)
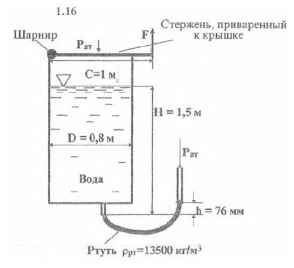
Требуется определить силу F, которую нужно приложить для приоткрывания крышки резервуара.
Решение (pdf) Решение (docx)Задача 1.18
Цена - 100 руб. (pdf) - 130 руб. (word)
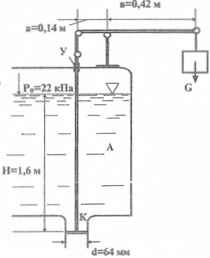
Грузовой клапан должен предотвращать превышение показанных на рисунке предельных значений глубины Н наполнения резервуара А жидкостью с плотностью ρ = 864 кг/м3 и избыточного давления р0. Определить, каким для этого должен быть вес груза G? Силу трения в уплотнении У стержня УК применять равной Т = 10 Н.
Решение (pdf) Решение (docx)Задача 1.20
Цена - 100 руб. (pdf) - 130 руб. (word)
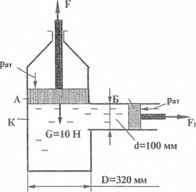
Определить:
1) наибольшую силу F, с которой поршень А может тянуть свой шток вниз при минимальном допустимом абсолютном давлении в рабочей камере К Рк = 20 кПа;
2) усилие F1, которое должно быть приложено к штоку поршня Б для создания в камере К такого давления.
Силу трения каждого поршня о стенки цилиндра считать равной 1/10 от силы давления на данный поршень.
Задача 1.23
Цена - 100 руб. (pdf) - 130 руб. (word)
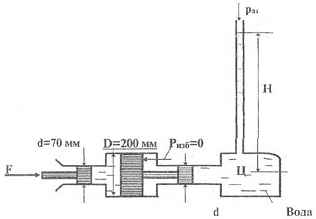
На рисунке представлена схема гиравлического повысителя давления. Определите усилие, которое нужно приложить к штоку поршня А, чтобы поднять воду из цилиндра Ц на высоту Н = 40 м.
Решение (pdf) Решение (docx)Задача 1.25
Цена - 100 руб. (pdf) - 130 руб. (word)
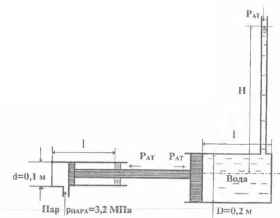
На рисунке представлена схема прямодействующего поршневого насоса. Требуется определить высоту подъема воды. Длина рабочей камеры l = 0,4 м.
Решение (pdf) Решение (docx)Задача 1.26
Цена - 100 руб. (pdf) - 130 руб. (word)
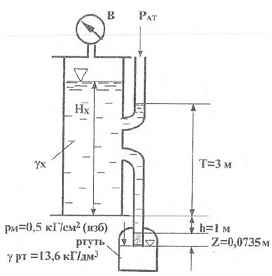
Используя приведенные на рисунке данные, определить высоту столба Нх и удельный вес γх жидкости в сосуде. Вакуумметр В показывает вакуумметрическую высоту hвак = 73,5 мм. рт.ст.
Решение (pdf) Решение (docx)Задача 1.28
Цена - 100 руб. (pdf) - 130 руб. (word)
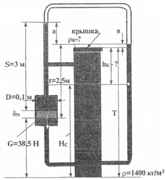
Определите плотность жидкости ρк и высоты столбов жидкости hк и жидкости НС. а = 0,56 м; в = 0,4 м; δN = 0,06 м; Т = 3,6 м.
Решение (pdf) Решение (docx)Задача 1.29
Цена - 100 руб. (pdf) - 130 руб. (word)
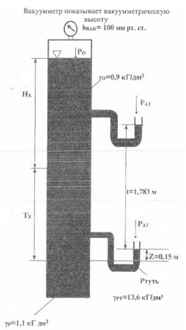
Вакуумметр показывает вакуумметрическую высоту hBAK = 100 мм. рт. ст. Используя приведенные на рисунке данные, определить высоты столбов Нх и Тх жидкостей.
Решение (pdf) Решение (docx)Задача 1.30
Цена - 100 руб. (pdf) - 130 руб. (word)
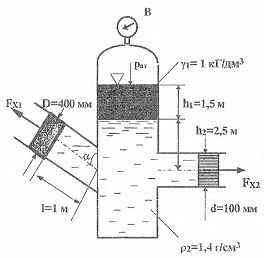
Используя приведенные на рисунке данные, определить силы Fх1 и Fх2, которые необходимо приложить к поршням, чтобы система находилась в равновесии. Вакуумметр В показывает вакуумметрическую высоту hвак = 150 мм.рт.ст. Угол наклона левой трубы 60 °.
Решение (pdf) Решение (docx)Задача 1.31
Цена - 100 руб. (pdf) - 130 руб. (word)
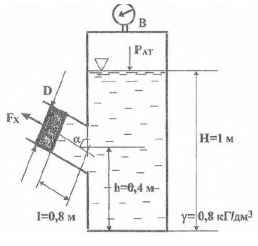
Используя приведенные на рисунке данные, определить силу Fх, которую необходимо приложить к поршню диаметром D = 250 мм, чтобы система находилась в равновесии. Вакуумметр В показывает вакуум метрическую высоту hвак = 37,5 мм. рт.ст. Угол наклона патрубка α = 30 °.
Решение (pdf) Решение (docx)Задача 1.32
Цена - 100 руб. (pdf) - 130 руб. (word)
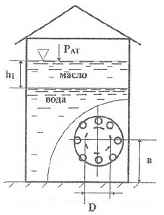
Высота уровня воды и масла в резервуаре 10 метров. Плотность масла 0,8 г/см3. На высоте в = 300 мм. от дна в резервуаре имеется отверстие диаметром D = 800 мм, крышка которого прикрепляется болтами диаметром 10 мм. Принимая для болтов допускаемое напряжение на разрыв 650 кГ/см2, определить необходимое число болтов. Определить также давление воды и масла на дно резервуара, если слой масла h1 = 2,5 м.
Решение (pdf) Решение (docx)Задача 1.33
Цена - 100 руб. (pdf) - 130 руб. (word)
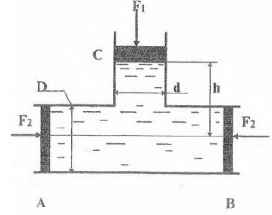
Труба диаметром D = 400 мм соединена с трубой диаметром d = 50 мм. Высота столба воды h = 80 см. В трубах имеются поршни. Какое усилие F2 нужно приложить на поршни А и В, чтобы система находилась в равновесии, если на поршень С действует сила F1 = 98,1 Н?
Решение (pdf) Решение (docx)Задача 1.34
Цена - 100 руб. (pdf) - 130 руб. (word)
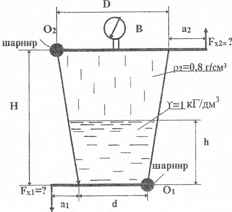
Используя приведенные на рисунке данные, определить силы Fx1 и Fx2, которые необходимо приложить к нижней и верхней крышкам сосуда, чтобы их открыть. Вакуумметр В показывает вакуумметрическую высоту hвак = 75 мм. рт. ст. Размеры: a1 = 60 см; а2 = 50 см; d = 1 м; D = 2 м; Н = 3 м; h = 1 м.
Решение (pdf) Решение (docx)Задача 1.37
Цена - 100 руб. (pdf) - 130 руб. (word)
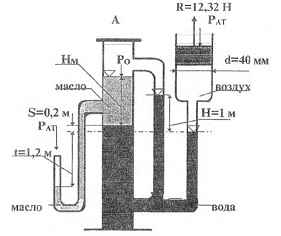
Используя приведенные на рисунке данные, определить давление РО в котле А, плотность ρм и высоту столба Нм масла.
Решение (pdf) Решение (docx)Задача 1.38
Цена - 100 руб. (pdf) - 130 руб. (word)
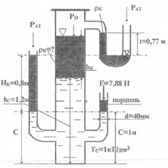
Используя приведенные на рисунке данные, определить давление РО на свободной поверхности жидкости плотность ρк, ее плотность и высоту столба этой жидкости hк.
Решение (pdf) Решение (docx)Задача 1.39
Цена - 100 руб. (pdf) - 130 руб. (word)
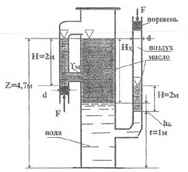
Используя приведенные на рисунке данные, определить высоты столбов Нх и hx жидкостей. γM = 0,8 кГ/дм3.
Решение (pdf) Решение (docx)Задача 1.40
Цена - 100 руб. (pdf) - 130 руб. (word)
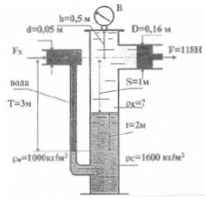
Показание вакуумметра В hвак = 75,5 мм. рт.ст. Используя приведенные на рисунке данные, определить плотность ρк жидкости и силу Fx, удерживающую представленную на рисунке гидравлическую систему в равновесии.
Решение (pdf) Решение (docx)Задача 1.41
Цена - 200 руб. (pdf) - 250 руб. (word)
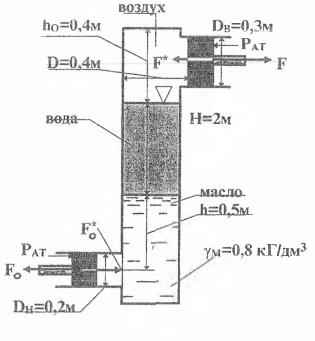
Задача 1.41. Определить силы F0 и F*0, которые должны быть приложены к нижнему поршню и его смещения Х и Х’ влево и вправо для создания вдоль штока верхнего поршня:
а) усилия F = 280 кГ, направленного вправо;
б) усилия F* = 280 кГ, направленного влево;
Исходное давление в воздушном пространстве при F = F* = 0 Рисх = Рат.
Исходные данные: h0 = 0,4 м; D = 0,4 м; Dв = 0,3 м; Н = 2 м; h = 0,5 м; γм = 0,8 кГ/дм3; γв = 9810 Н/м3.
Задача 1.43
Цена - 100 руб. (pdf) - 130 руб. (word)
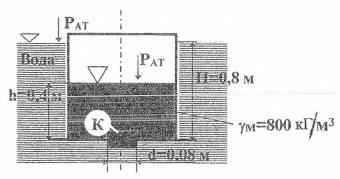
Задача 1.43. Какой вес должен иметь клапан К чтобы в условиях, показанных на рисунке, он не открывался?
Исходные данные: h = 0,4 м; d = 0,08 м; Н = 0,8 м; γм = 800 кГ/м3.
Задача 1.49
Цена - 100 руб. (pdf) - 130 руб. (word)
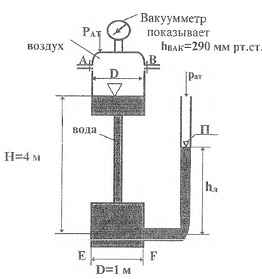
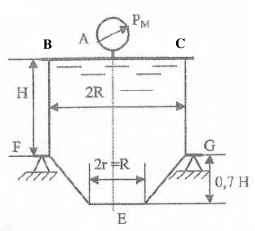
Вакуумметр показывает hвак = 290 мм. рт.ст. Определить высоту столба воды hx в пьезометре П, присоединенном к изображенной на рисунке системе, и силы суммарного давления воздуха и воды на крышку АВ и дно EF.
Решение (pdf) Решение (docx)Задача 1.52
Цена - 100 руб. (pdf) - 130 руб. (word)
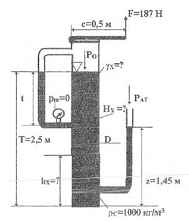
Используя приведенные на рисунке данные, определить высоты столбов Нх и hx жидкостей, а также удельный вес γх верхней жидкости, если система находится в равновесии под действием силы F, приложенной к крышке колонны. Определить также давление р0 на свободной поверхности жидкости. t = 1 м; D = 0,3 м.
Решение (pdf) Решение (docx)Задача 1.53
Цена - 100 руб. (pdf) - 130 руб. (word)
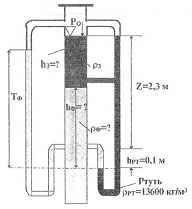
Используя приведенные на рисунке данные, определить высоты столбов hз и hф жидкостей, а также плотность ρф нижней жидкости. ρз = 800 кг/м3; Тф = 2 м.
Решение (pdf) Решение (docx)Задача 1.54
Цена - 100 руб. (pdf) - 130 руб. (word)
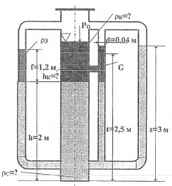
Используя приведенные на рисунке данные, определить плотности ρк и ρс жидкостей, а также высоту столба hк верхней жидкости в сосуде. В правой трубке находится в равновесии поршень весом G = 10 Н; ρз = 1000 кг/м3.
Решение (pdf) Решение (docx)Задача 1.56
Цена - 100 руб. (pdf) - 130 руб. (word)
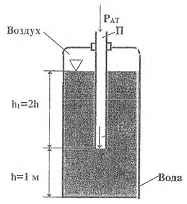
1. Определить силы суммарного давления воздуха: а) снаружи и изнутри на крышку резервуара; б) воды и наружного воздуха на дно резервуара.
2. Решить ту же задачу для случая, когда нижний конец пьезометра П опущен до дна и весь пьезометр заполнен атмосферным воздухом.
Задача 1.57
Цена - 100 руб. (pdf) - 130 руб. (word)
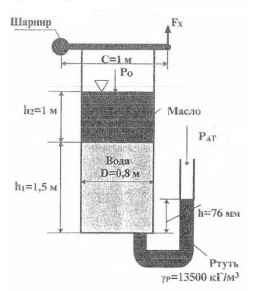
Определить усилие Fx, которое необходимо приложить к крышке резервуара для ее приоткрывания.
Решение (pdf) Решение (docx)Задача 1.58
Цена - 100 руб. (pdf) - 130 руб. (word)
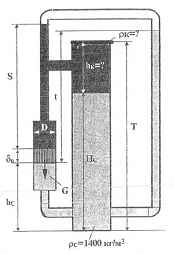
Используя приведенные на рисунке данные, определить высоты столбов hк и Нс жидкостей, а также плотность ρк верхней жидкости в сосуде. δп = 0,06 м; D = 0,1 м; G = 38,5 Н; t = 3 м; S = 2,5 м; Т = 3,6 м; hс = 1,5 м.
Решение (pdf) Решение (docx)Задача 1.59
Цена - 100 руб. (pdf) - 130 руб. (word)
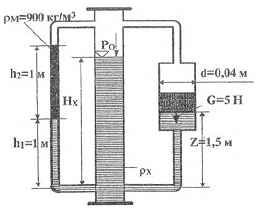
Используя приведенные на рисунке данные, определить высоту столба Нх жидкости, а также ее плотность ρх.
Решение (pdf) Решение (docx)Задача 1.62
Цена - 100 руб. (pdf) - 130 руб. (word)
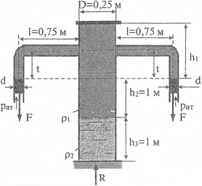
Используя приведенные на рисунке данные, определить реакцию R, а также равнодействующие Fg и FKР всех сил, действующих соответственно на дно и крышку баллона. Собственный вес баллона G = 1000 H.
t = 0,25 м; d = 0,05 м; F = 96 H; p1 = 900 кг/м3; p2 = 1100 кг/м3; h1 = 0,5 м.
Задача 1.64
Цена - 100 руб. (pdf) - 130 руб. (word)
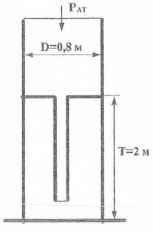
Тетрахлорметан, плотность которого ρ = 1600 кг/м3, должен быть залит в показанный на рисунке резервуар в количестве V = 1,0048 м3. До заливки жидкости в резервуар абсолютное давление в обоих отсеках резервуара равнялось атмосферному. Как жидкость распределится между верхним и нижним отсеками резервуара?
Примечание: Внутренним диаметром центральной трубки пренебречь.
Задача 1.65
Цена - 100 руб. (pdf) - 130 руб. (word)
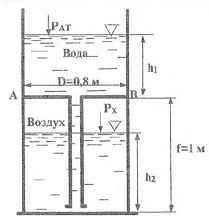
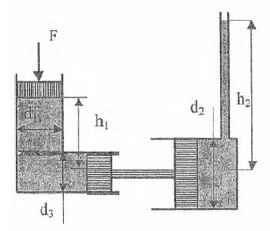
Вычислить силу суммарного гидростатического давления воды и воздуха на днище АВ. Предварительно определить толщину h2 слоя воды, которая стечет в нижнюю часть резервуара, учитывая при этом, что сумма глубин наполнения водой, залитой в резервуар, его верхней и нижней частей h1 + h2 = f = 1 м. Процесс сжатия воздуха под днищем АВ при отекании воды считать изотермическим.
Решение (pdf) Решение (docx)Задача 1.66
Цена - 100 руб. (pdf) - 130 руб. (word)
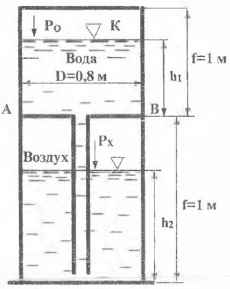
Вычислить силу суммарного гидростатического давления воды и воздуха на днище АВ после того, как в показанный на рисунке закрытый резервуар при первоначальном абсолютном давлении в нем, равном атмосферному, насосом через камеру К будет подана вода, суммарная высота столба которой равна f = 1 м.
Решение (pdf) Решение (docx)Задача 1.67
Цена - 100 руб. (pdf) - 130 руб. (word)
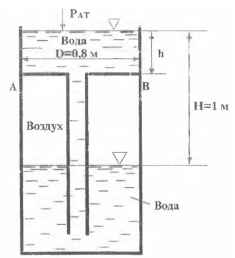
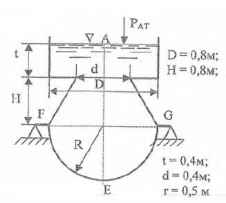
Вычислить силу суммарного гидростатического давления воды и воздуха на днище АВ.
h = 0,5 м; D = 0,8 м.
Задача 1.73
Цена - 100 руб. (pdf) - 130 руб. (word)
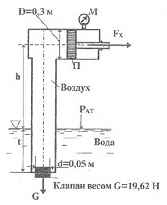
Манометр М показывает манометричесское давление рм = З кГ/см2. Требуется определить силу Fx, удерживающую поршень П в покое.
t = l м; h = 5 м.
Задача 1.77
Цена - 100 руб. (pdf) - 130 руб. (word)
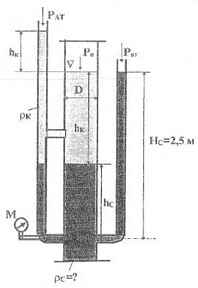
hк = 1,5 м; D = 0,5 м; hс = 1 м. Показание манометра М рм = 0,4 кГ/см2. Требуется определить:
1) плотности ρк и ρс жидкостей;
2) давление Рo;
3) равнодействующую сил давления воздуха на крышку котла снизу и сверху.
Задача 1.78
Цена - 100 руб. (pdf) - 130 руб. (word)
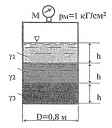
В закрытом резервуаре содержатся три разных жидкости. Высота каждого слоя h = 0,5 м; удельные веса каждой из жидкостей составляют: γ1 = 0,8 кГ/ДМ3; γ2 =1 Г/ДМ3; γ3 = 1,5 Г/ДМ3. Учитывая показания присоединенного к резервуару манометра М, определить,чему равна разность сил суммарного гидростатического давления на крышку и дно резервуара?
Решение (pdf) Решение (docx)Задача 1.81
Цена - 100 руб. (pdf) - 130 руб. (word)
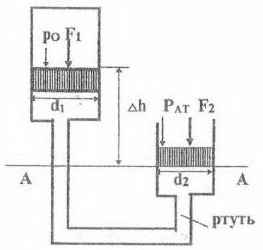
Определить Δh - разность в высотном положении поршней в сообщающихся цилиндрах, если диаметры цилиндров d1 = 30 см; d2 = 20 см. Нагрузки на поршни F1 = 120 кГ, F2 = 20 кГ, абсолютное давление в закрытом левом цилиндре над поршнем ро = 0 кГ/см2. В цилиндры и соединительные трубки налита ртуть γрт = 13,6 кГ/ДМ3.
Решение (pdf) Решение (docx)Задача 1.82
Цена - 100 руб. (pdf) - 130 руб. (word)
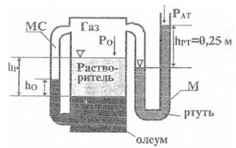
К закрытому резервуару, содержащему растворитель и олеум (γо = 2000 кГ/м3), присоединено мерное стекло МС и ртутный манометр М. Используя их показания, определить удельный вес растворителя и давление на его поверхности. ho = 0,5 м; hP = 1 м.
Решение (pdf) Решение (docx)Задача 1.83
Цена - 100 руб. (pdf) - 130 руб. (word)
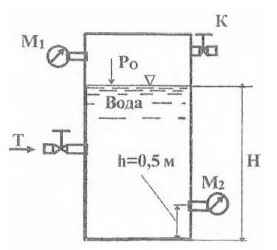
Закрытый цилиндрический резервуар сообщается с водопроводной сетью трубкой Т и с атмосферой краном К. До половины резервуар наполняется при открытом кране К, после чего кран закрывается и при дальнейшем наполнении давление на уровне манометра М2 доводится до p2 = 1,125 ати. Определить давление Ро на поверхности воды в резервуаре в этот момент. Н = 3 м; h = 0,5 м.
Решение (pdf) Решение (docx)Задача 1.84
Цена - 100 руб. (pdf) - 130 руб. (word)
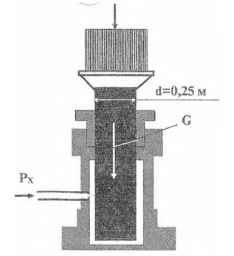
Определить:
1) давление Рх, которое необходимо подводить к гидравлическому аккумулятору для подъема груза G = 10 T;
2) работу и мощность, затрачиваемые насосом при подъеме груза G на высоту 2 м в течение 10 с;
3) подачу насоса в единицу времени.
Задача 1.85
Цена - 100 руб. (pdf) - 130 руб. (word)
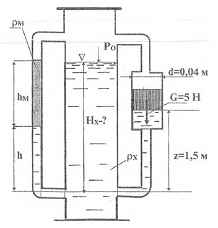
Используя приведенные на рисунке данные, определить плотность жидкости в сосуде рх и высоту столба этой жидкости в сосуде Нх.
ρм = 900 кг/м3; h = 1 м; hм = 1 м.
Задача 1.86
Цена - 100 руб. (pdf) - 130 руб. (word)
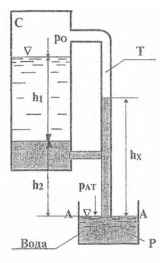
При каком давлении рo в сосуде С вода, втянутая в сосуд из резервуара Р, будет поддерживать слой жидкости h1 удельного веса γж = 0,9 кГ/л на высоте h2 = 1,64 м над уровнем А-А? На какую высоту hx поднимется при этом вода по трубке Т?
h1 = 0,4 м; h2 = 1,64 м.
Задача 1.87
Цена - 100 руб. (pdf) - 130 руб. (word)
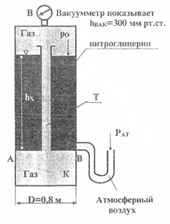
Вакуумметр показывает hвак = 300 мм. рт.ст. Закрытый резервуар, к которому присоединены вакуумметр В и U-образная трубка, заполнен нитроглицерином (γH = 1,6 кГ/дм3). Под резервуаром имеется камера К, сообщающаяся трубкой Т с верхней частью внутреннего пространства резервуара. Используя приведенные на рисунке данные, определить высоту столба hx нитроглицерина и суммарную силу гидростатического давления жидкости и газа на крышку АВ камеры К.
Решение (pdf) Решение (docx)Задача 1.88
Цена - 100 руб. (pdf) - 130 руб. (word)
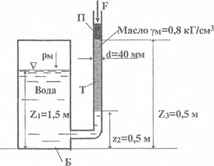
Вывести зависимость между избыточным давлением на свободной поверхности воды в закрытом баке Б и усилием F, которое должно быть приложено к поршеньку П в трубке Т для удержания всей системы в равновесии. Вычислить усилие F для случая, когда рм = 0.
Решение (pdf) Решение (docx)Задача 1.89
Цена - 100 руб. (pdf) - 130 руб. (word)
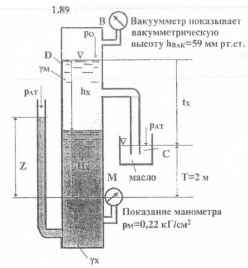
Используя приведенные на рисунке данные, определить:
1) удельный вес γх нижней жидкости в сосуде;
2) превышение tx уровня масла в трубе D над уровнем в сосуде C;
3) высоты столбов масла hx и Нх жидкости удельного веса γх.
Z = 2 м; γм = 0,8 кГ/ДМ3.
Задача 1.91
Цена - 100 руб. (pdf) - 130 руб. (word)
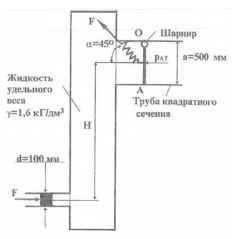
Используя приведенные на рисунке данные, определить величину силы натяжения пружины F, при которой клапан ОА не поворачивался бы вокруг шарнира О.
F = 37,68 кГ; Н = 3 м.
Задача 1.93
Цена - 100 руб. (pdf) - 130 руб. (word)
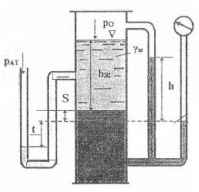
Используя приведенные на рисунке данные, определить давление ро в котле А, удельный вес γж и высоту столба hж верхней жидкости в котле.
Вакуумметр показывает hBАК = 76 мм. рт.ст. h = 1 м; S = 0,2 м; t = 1,2 м. Жидкость удельного веса у = 1 кГ/дм3.
Задача 1.94
Цена - 100 руб. (pdf) - 130 руб. (word)
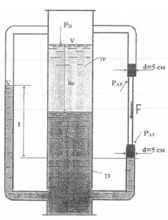
Требуется определить удельные веса γр и γ3 жидкостей, при которых для удержания изображенной на рисунке системы в равновесии потребуется к соединяющему поршни штоку приложить силу F = 4,4 кГ.
hp = 1,25 м; hз = 1 м; t = 1,83 м.
Задача 1.95
Цена - 100 руб. (pdf) - 130 руб. (word)
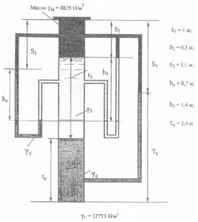
Используя приведённые на рисунке данные, определить удельный вес γз верхней жидкости и высоты столбов tз и tc верхней и нижней жидкостей.
Решение (pdf) Решение (docx)Задача 1.96
Цена - 100 руб. (pdf) - 130 руб. (word)
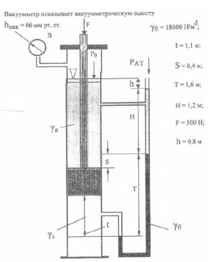
Используя приведённые на рисунке данные, определить удельные веса верхней γк и нижней γс жидкостей. Диаметр поршня D = 0,35 м.
Решение (pdf) Решение (docx)Задача 1.97
Цена - 100 руб. (pdf) - 130 руб. (word)
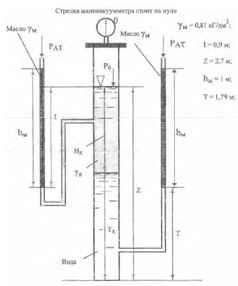
Используя приведённые на рисунке данные, определить удельный вес γВ в верхней жидкости и высоты столбов верхней жидкости Hх и воды Тх. Стрелка мановакуумметра стоит на нуле.
Решение (pdf) Решение (docx)Задача 1.98
Цена - 100 руб. (pdf) - 130 руб. (word)
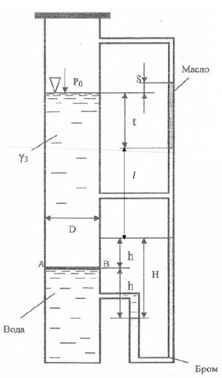
Используя приведённые на рисунке данные, определить удельный вес γз верхней жидкости в сосуде и диаметр резервуара D, при котором равнодействующая сил давления верхней жидкости (сверху) и воды (снизу) на диафрагму (промежуточное днище) АВ не превысит 1500 Н.
Решение (pdf) Решение (docx)Задача 1.99
Цена - 100 руб. (pdf) - 130 руб. (word)
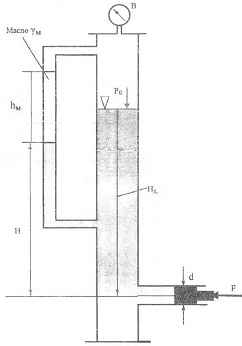
Используя приведённые на рисунке данные, определить удельный вес γх и высоту столба Нх жидкости в сосуде. Вакуумметр показывает вакуумметрическую высоту hВАК = 600 мм рт. ст.
Решение (pdf) Решение (docx)Задача 1.100
Цена - 100 руб. (pdf) - 130 руб. (word)
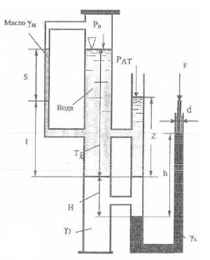
Используя приведённые на рисунке данные, определить давление Ро, высоту Тх столба воды и удельный вес γз нижней жидкости в сосуде.
Решение (pdf) Решение (docx)1.4. МНОГОВАРИАНТНЫЕ ЗАДАЧИ
Задача 1
Задача 1
Цена - 100 руб. (pdf) - 120 руб. (word)
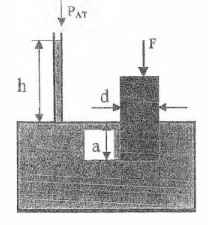
Определить, на какую высоту h поднимется вода в пьезометрической трубке под действием плунжера при следующих данных: диаметр плунжера d, заглубление плунжера а, сила давления F. Собственный вес плунжера не учитывать.
Задача 2
Цена - 100 руб. (pdf) - 120 руб. (word)
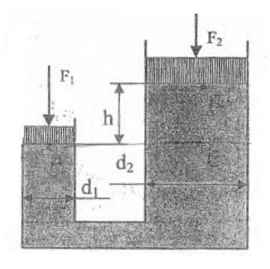
На поршень одного из сообщающихся сосудов, наполненных водой, действует сила F1. Какую силу F2 нужно приложить ко второму поршню, чтобы уровень воды по ним был на h метров выше уровня воды над первым поршнем. Диаметр первого поршня d1, диаметр второго поршня d2.
Задача 3
Цена - 100 руб. (pdf) - 120 руб. (word)
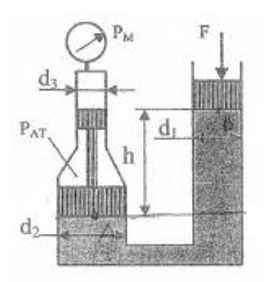
Определить манометрическое давление Рм в верхней части одного из сообщающихся сосудов, заполненных водой, под действием силы F, приложенной к поршню правого сосуда.
Задача 4
Цена - 100 руб. (pdf) - 120 руб. (word)
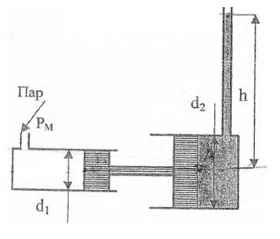
Определить высоту h, на которую может поднять воду прямодействующий паровой насос при следующих данных: диаметр парового цилиндра d1, манометрическое давление в паровом цилиндре рм.
Задача 6
Цена - 100 руб. (pdf) - 120 руб. (word)
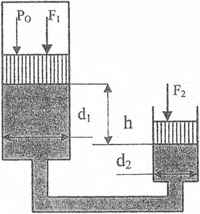
Определить разность в высотном положении поршней в сообщающихся цилиндрах h если известны: диаметры цилиндров d1 и d2; нагрузки на поршни F1 и F2; избыточное давление в закрытом левом цилиндре над поршнем Ро. В цилиндры и соединительную трубку налита ртуть. γрт = 13,6 Т/м3.
| Вариант | d1, cм | d2, cм | F1, кГ | F2, кГ | Po, кГ/см2 | Решение: |
|---|---|---|---|---|---|---|
| Вариант 7 | 50 | 20 | 140 | 25 | 2 | PDF 7 |
Задача 7
Цена - 100 руб. (pdf) - 120 руб. (word)
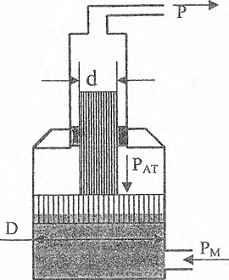
Определить давление Р, получаемое в гидравлическом мультипликаторе, если Масло подается под поршень под манометрическим давлением рм. Размеры мультипликатора: диаметры поршня D и штока d приведены в таблице в зависимости от номера варианта. Удельный вес масла γМ = 0,8 Г/см3.
Задача 8
Цена - 100 руб. (pdf) - 120 руб. (word)

В цилиндрическом резервуаре имеется диафрагма АВ с приваренной к ней трубой Т. Размеры резервуара: Dц = 200 мм; D = 400 мм; h = 0,6 + 0,4·√N, м; t = 0,6 + 0,2·√N, м. Требуется определить:
1) толщину слоя воды С на дне резервуара, заполненного в верхней части до уровня ЕК, когда абсолютное давление на свободной поверхности воды равно атмосферному;
2) силу F, которую нужно приложить к показанному на рисунке пунктиром поршню П, чтобы половина пространства под диафрагмой была заполнена водой. Чему будет равно при этом смещение S поршня относительно уровня ЕК?
3) силу F*, которую нужно приложить к поршню, чтобы поднять затем всю воду из нижней части резервуара в пространство над диафрагмой.
Вес поршня G = 200 Н. До вливания воды весь резервуар был заполнен атмосферным воздухом. Процесс сжатия и расширения воздуха в пространстве под диафрагмой считать изотермическим.
| Вариант | h, м | t, м | Решение: |
|---|---|---|---|
| Вариант 9 | 1,8 | 1,2 | PDF 9 |
Задача 9
Цена - 100 руб. (pdf) - 120 руб. (word)

По показаниям мановакуумметра В и манометра М определить усилие F, которое будет удерживать систему в равновесии. Рисунок гидравлической системы представлен на следующей странице.
Дано: показания мановакуумметра В: при N нечетном hвак = 20(N - 1), мм. рт. ст.; при N четном Рм = 0,05 N, кГ/см2; показания манометра М: h = 7,2 – 0,2N, дм; D2 = 50 + 20∙lgN, мм; D1 = 2,5D2; d = 0,4D2. Сила трения, действующая на каждый поршень составляет 10 % от суммарной силы давления на поршень. ρрт = 13500 кг/м3; ρхл = 1500 кг/м3.
| Вариант | Рм, кГ/см2 | h, дм | D2, мм | Решение: |
|---|---|---|---|---|
| Вариант 8 | 0,4 | 5,6 | 68 | PDF 8 |
2. ОПРЕДЕЛЕНИЕ СУММАРНОЙ СИЛЫ ГИДРОСТАТИЧЕСКОГО ДАВЛЕНИЯ НА ПЛОСКИЕ ПОВЕРХНОСТИ
2.3. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Задача 2.1
Цена - 130 руб. (pdf) - 160 руб. (word)
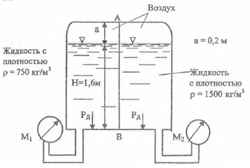
Используя приведенные на рисунке данные, определить величину и точку приложения равнодействующей силы давления жидкостей и воздуха на перегородку АВ, ширина которой b = 1,2 м. Согласно показаниям манометров, избыточное давление на дно сосуда одинаково по обе стороны перегородки и равно М1 и М2 избыточное давление на дне резервуара одинаково по обе стороны перегородки и равно РД = 12 кПа.
Решение (pdf) Решение (docx)Задача 2.2
Цена - 130 руб. (pdf) - 160 руб. (word)
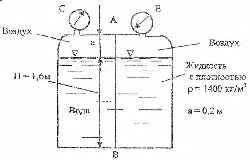
Мановакуумметры С и Е показывают: левый – манометрическое давление рм = 5 кПа, правый – вакууметрическую высоту h = 10,3 мм.рт.ст. Определить величину и точку приложения равнодействующей силы давления жидкостей и воздуха на стенку АВ. Ширина стенки b = 0,9 м.
Решение (pdf) Решение (docx)Задача 2.4
Цена - 130 руб. (pdf) - 160 руб. (word)
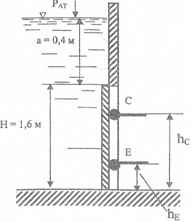
Отверстие в стенке водохранилища шириною b = 2 м. перекрывается плоским щитом. Ригели G и Е, на которые опирается щит, должны воспринимать одинаковую нагрузку. Какими для этого должны быть высоты расположения ℎ𝐶 и ℎ𝐸 ригелей?
Решение (pdf) Решение (docx)Задача 2.5
Цена - 130 руб. (pdf) - 160 руб. (word)
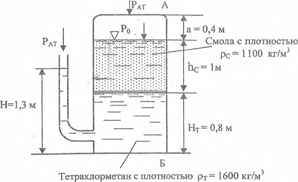
Используя приведенные на рисунке данные, определить величину и точку приложения равнодействующей сил давления жидкостей и воздуха на стенку АБ резервуара, имеющего форму параллелепипеда. Ширина стенки b =0,9 м.
Решение (pdf) Решение (docx)Задача 2.6
Цена - 130 руб. (pdf) - 160 руб. (word)
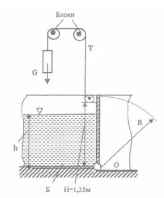
Для автоматического регулирования глубины наполнения бассейна Б водой проектируется изображенный на рисунке затвор в форме прямоугольного щита шириною b = 1,35 м. Определить величину груза G, который должен быть подвешен к тросу Т, чтобы щит опускался, поворачиваясь вокруг шарнира О, когда глубина воды в бассейне будет превышать h = 1,2 м.
Решение (pdf) Решение (docx)Задача 2.7
Цена - 130 руб. (pdf) - 160 руб. (word)
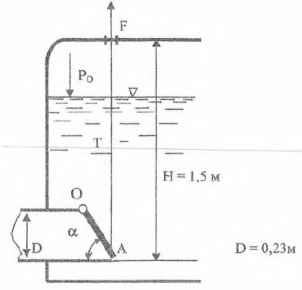
Клапан ОА закрывает входное отверстие трубы, через которое из бензохранилища выпускается бензин, избыточное давление на поверхности которого равно РО = 5 кПа. Плотность бензина ρ = 700 кг/м3. Определить угол α наклона клапана к горизонту, при котором прикладываемая для открывания клапана к тросу Т сила F его натяжения не превысит 824 Н.
Решение (pdf) Решение (docx)Задача 2.8
Цена - 130 руб. (pdf) - 160 руб. (word)
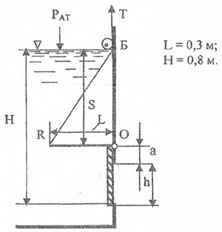
Отверстие высотой h = 0,2 м и шириной b = 0,5 м в стенке открытого резервуара перекрывается щитом, подвешенным к горизонтальной оси О. Для выпуска воды из резервуара щит поворачивается вокруг оси О с помощью троса, прикрепленного к рычагу R и отклоняемого к стенке резервуара блоком Б. Определить, при каком расстоянии S от оси О до блока Б усилие T, которое нужно приложить к тросу для поворота щита вокруг оси О, будет равно 380 Н. Расстояние от верхней кромки отверстия до оси О a = 0,05 м.
Решение (pdf) Решение (docx)Задача 2.11
Цена - 130 руб. (pdf) - 160 руб. (word)
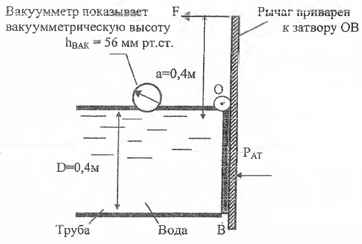
Определите усилие F, которое нужно приложить к рычагу, чтобы повернуть затвор ОВ вокруг оси О для выпуска воды из трубы.
Решение (pdf) Решение (docx)Задача 2.13
Цена - 180 руб (pdf) - 200 руб. (word)
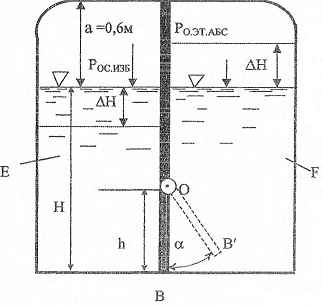
На рисунке представлено состояние гидравлической системы, при котором щит ОВ’ выведен из его устойчивого отвесного положения и через отверстие ОВ происходит перетекание суспензии (краски) из отсека резервуара Е в отсек F. Однако система стремится к устойчивому равновесию, при котором щит займет вертикальное положение, и перетекание суспензии прекратится. Определить, какими к моменту достижения равновесного состояния системы должны быть величины: 1) Смещение ΔН уровней жидкости в обоих отсеках (площади свободной поверхности жидкости в отсеках одинаковы); 2) Давления Р’ос и Р’оэт на свободной поверхности соответственно суспензии и растворителя. Процессы расширения воздуха в отсеке Е над суспензией и сжатия воздуха в отсеке F над растворителем считать изотермическими.
Решение (pdf) Решение (docx)Задача 2.14
Цена - 130 руб. (pdf) - 160 руб. (word)
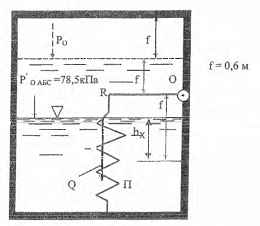
В стенке резервуара, содержащего раствор с плотностью ρ = 1300 кг/м3, имеется отверстие шириной b = 0,9 м, перекрываемое щитом, висящим на оси О и прижимаемым к стенке резервуара посредством рычага OR длиною l = 0,6 м и прикрепленной к его концу пружины П. Сила натяжения пружины Q = 4,9 кН. При откачке раствора из резервуара наступает момент, когда щит начинает отходить от стенки и пропускать через отверстие воздух и раствор.
Определить: 1) предельное возвышение hx свободной поверхности раствора над нижней кромкой щита, после достижения которого дальнейшая откачка раствора из резервуара будет сопровождаться притоком в него воздуха извне и утечкой раствора через отверстие;
2) начальное давление воздуха Р0 в резервуаре.
Процесс расширения воздуха в резервуаре при откачке из него раствора считать изотермическим.
Исходные данные: ρ = 1300 кг/м; b = 0,9 м; l = 0,6 м; Q = 4,9 кН; f = 0,6 м
Задача 2.15
Цена - 130 руб. (pdf) - 160 руб. (word)
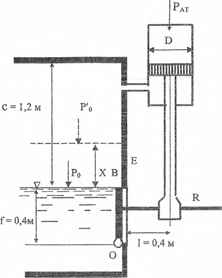
Наполнение резервуара Е водой регулируется цилиндром с поршнем диаметром D = 0,29 м и весом G = 166 Н.На рисунке показано начальное положение свободной поверхности воды, когда абсолютное давление РО воздуха над нею равно атмосферному давлению. Повышение уровня воды при нагнетании ее в резервуар сопровождается изотермическим сжатием воздуха в пространстве над водой, вследствие чего наступает момент, когда поршень оказывается в состоянии повернуть рычаг R и щит ВО вокруг оси О и прекратить дальнейшее повышение уровня воды в резервуаре. Определить смещение Х уровня воды в резервуаре и давление Р’О, превышение которых будет вызывать поворот щита вокруг оси О и истечение воды через отверстие, которое перед этим было перекрыто щитом ВО. Ширина щита b = 0,3 м.
Решение (pdf) Решение (docx)Задача 2.16
Цена - 130 руб. (pdf) - 160 руб. (word)
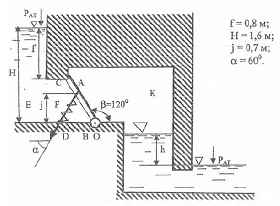
Поворотный щит АО шириной b = 1 м, перекрывающий водоспускное отверстие в теле гидросооружения, прижимается к опорной раме В пружиной С, сила натяжения которой F = 10 кН. Определить наименьшую разность уровней h воды в камере К и в отводящем русле, при которой щит отойдет от опорной рамы и вода из камеры Е начнет поступать через отверстие AD в камеру К.
Решение (pdf) Решение (docx)Задача 2.20
Цена - 130 руб. (pdf) - 160 руб. (word)
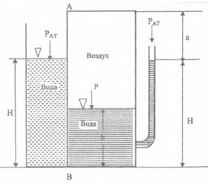
Используя приведенные на рисунке данные, определить величину и точку приложения равнодействующей сил давления воды и воздуха на перегородку АВ, ширина которой b = 1,5 м.
Н = 1,8 м; h = 0,9 м; а = 0,3 м.
Задача 2.22
Цена - 130 руб. (pdf) - 160 руб. (word)
Используя приведенные на рисунке данные, определить величину и точку приложения равнодействующей сил давления жидкостей на перегородку АВ, ширина которой b = 0,9 м. Н = 1,2 м; h = 0,9 м.
Решение (pdf) Решение (docx)Задача 2.23
Цена - 130 руб. (pdf) - 160 руб. (word)
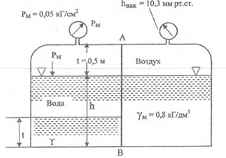
Определить величину и точку приложения равнодействующей сил давления жидкостей и воздуха на стенку АВ. Ширина стенки b = 0,9 м. Вакуумметр показывает вакуумметрическую высоту hвак = 10,3 мм. рт.ст.
t = 0,8 м; h = 1,6 м; γ = 1,4 кГ/дм3.
Задача 2.24
Цена - 130 руб. (pdf) - 160 руб. (word)
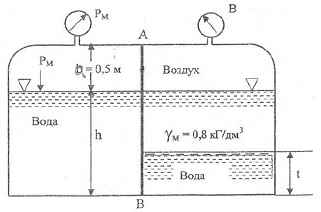
Определить величину и точку приложения равнодействующей сил давления жидкостей и воздуха на стенку АВ. Ширина стенки b = 0,9 м. Вакуумметр B показывает вакуумметрическую высоту hвак = 10,3 мм. рт.ст.
t = 0,8 м; h = 1, 6 м.
Задача 2.25
Цена - 200 руб. (pdf) - 250 руб. (word)
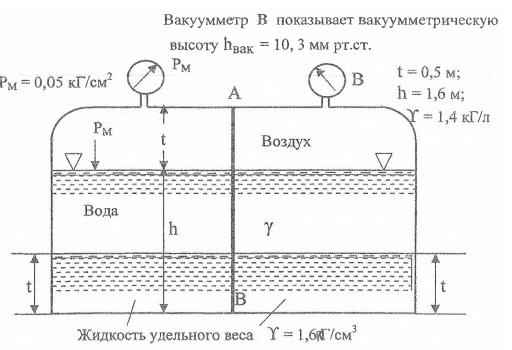
Определить величину и точку приложения суммарной силы давления жидкостей и воздуха на перегородку АВ, ширина которой b = 0,9 м.
Решение (pdf) Решение (docx)Задача 2.26
Цена - 130 руб. (pdf) - 160 руб. (word)
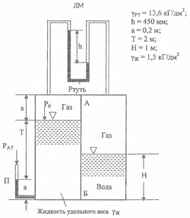
Используя показания пьезометра П и дифференциального манометра ДМ определить:
1) давление РО на поверхности жидкости;
2) результирующую сил давления на перегородку АБ жидкости и газов (слева и справа). Ширина перегородки b = 1,5 м.
Рисунки к задачам приведены на последующих страницах. Дополнительные исходные данные представлены на соответствующих схемах (рисунках).
Исходные данные: γрт = 13,6 кГ/дм3; h = 450 мм; a = 0,2 м; T = 2 м; H = 1 м; γж = 1,5 кГ/дм3.
Задача 2.27
Цена - 130 руб. (pdf) - 160 руб. (word)
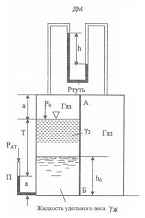
Используя показания пьезометра П и дифференциального манометра ДМ определить:
1) давление РО на поверхности жидкости;
2) результирующую сил давления на перегородку АБ жидкости и газов (слева и справа). Ширина перегородки b = 1,5 м.
Исходные данные: a = 0,2 м; h = 450 мм; Т = 2 м; h0 = 1 м; γж = 1,5 кГ/дм3; γ2 = 1,0 Г/cм3; b = 1,5 м
Задача 2.29
Цена - 130 руб. (pdf) - 160 руб. (word)
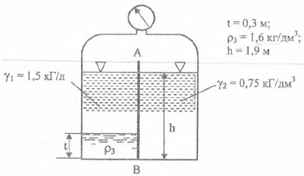
Определить величину и точку приложения равнодействующей сил давления жидкостей и воздуха на стенку АБ. Ширина стенки b = 1,2 м.
Рисунки к задачам приведены на последующих страницах. Дополнительные исходные данные представлены на соответствующих схемах (рисунках).
Вакуумметр показывает hBAK = 147 мм рт.ст; t = 0,3 м; ρз = 1,6 кг/дм3; h = 1,9 м.
Задача 2.31
Цена - 130 руб. (pdf) - 160 руб. (word)
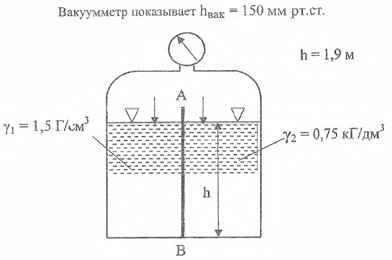
Определить величину и точку приложения равнодействующей сил давления жидкостей и воздуха на стенку АБ. Ширина стенки b = 1,2 м.
Рисунки к задачам приведены на последующих страницах. Дополнительные исходные данные представлены на соответствующих схемах (рисунках).
Вакуумметр показывает hBAK = 150 мм рт.ст; h = 1,9 м.
Задача 2.35
Цена - 130 руб. (pdf) - 160 руб. (word)
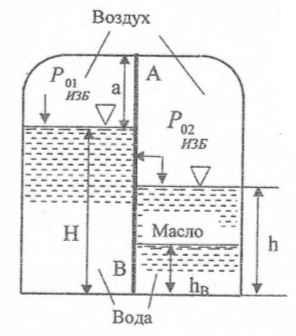
Используя приведенные на рисунке данные, определить величину и точку приложения равнодействующей сил давления воды и воздуха на перегородку АВ, ширина которой b = 1,5 м.
h = 0,9 м; РO2,ИЗБ = 0,09 кГ/см2; РO1,ИЗБ = 0; Н = 1,8 м; а = 0,3 м; ρм = 0,8 г/см3; hВ = 0,45 м.
Задача 2.36
Цена - 130 руб. (pdf) - 160 руб. (word)
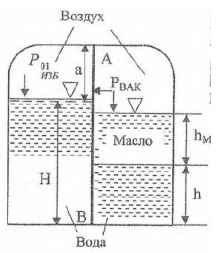
Используя приведенные на рисунке данные, определить величину и точку приложения равнодействующей сил давления воды и воздуха на перегородку АВ, ширина которой b = 1,5 м.
h = 0,9 м; РO1,ИЗБ = 0,2 ат; Н = 1,8 м; а = 0,3 м; ρм = 0,8 г/см3; hм = 0,45 м; Рвак = 75 мм.рт.ст.
Задача 2.39
Цена - 130 руб. (pdf) - 160 руб. (word)
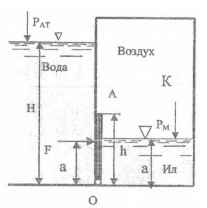
Определить силу F, которую нужно приложить к прямоугольной формы щитку АО высотой h = 0,6 м и шириной b = 0,4 м, чтобы повернуть его вокруг шарнира О для впуска воды в камеру К.
Рм = 0,2 кГ/см2; Н = 1,4 м; а = 0,4 м; h = 0,6 м; ρил = 1,2 кг/л.
Задача 2.41
Цена - 130 руб. (pdf) - 160 руб. (word)
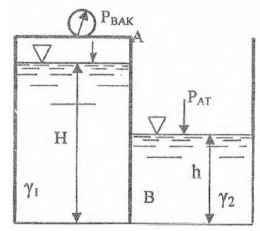
Используя приведенные на рисунке данные, определить величину и точку приложения равнодействующей сил давления жидкостей на перегородку АВ, ширина которой b = 0,9 м.
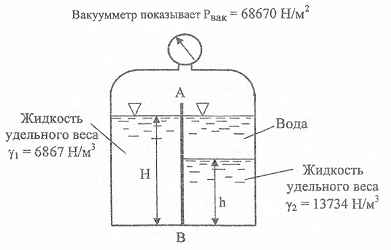
Рвак = 68670 Па; Н = 1,2 м; h = 0,6 м; γ1 = 6867 Н/м3; γ2 = 13734 Н/м3.
Задача 2.42
Цена - 130 руб. (pdf) - 160 руб. (word)
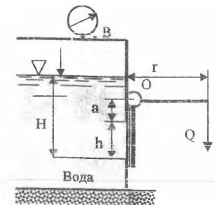
Прямоугольное отверстие высотой h = 0,3 м и шириной b = 0,5 м в вертикальной стенке закрытого резервуара закрыто щитом, вращающимся вокруг горизонтальной оси О и прижимаемых посредством двух грузов, подвешенных на рычагах r = 0,4 м. Определить минимальный вес каждого груза, если расстояние от верхней кромки отверстия до оси вращения щита а = 50 мм. Весом рычагов и трением в подшипниках пренебречь. Вакуумметр В показывает hвак = 52,25 мм.рт.ст.
Решение (pdf) Решение (docx)Задача 2.43
Цена - 130 руб. (pdf) - 160 руб. (word)
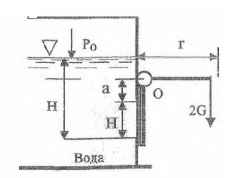
Прямоугольное отверстие высотой h = 0,03 м и шириной b = 0,3 м в вертикальной стенке закрытого резервуара закрыто щитом, вращающимся вокруг горизонтальной оси О и прижимаемых посредством двух грузов, каждый весом G = 50 кГ, подвешенных на рычагах r = 0,3 м. Определить предельное значение давления РО, при превышении которого произойдет утечка воды через отверстие. Глубина погружения нижней кромки отверстия Н = 1,5 м, а расстояние от верхней кромки отверстия до оси щита а = 50 мм. Весом рычагов и трением в подшипниках пренебречь.
Решение (pdf) Решение (docx)Задача 2.45
Цена - 130 руб. (pdf) - 160 руб. (word)
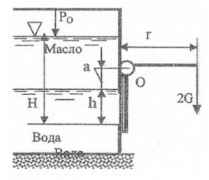
Прямоугольное отверстие высотой h = 0,03 м и шириной b = 0,3 м в вертикальной стенке закрытого резервуара закрыто щитом, вращающимся вокруг горизонтальной оси О и прижимаемых посредством двух грузов, каждый весом G = 50 кГ, подвешенных на рычагах r = 0,3 м. Определить предельное значение давления РО, при превышении которого произойдет утечка воды через отверстие. Глубина погружения нижней кромки отверстия Н = 1,5 м, а расстояние от верхней кромки отверстия до оси щита а = 50 мм. Весом рычагов и трением в подшипниках пренебречь.
Решение (pdf) Решение (docx)Задача 2.47
Цена - 130 руб. (pdf) - 160 руб. (word)
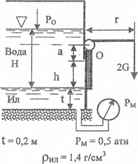
Прямоугольное отверстие высотой h = 0,3 м и шириной b = 0,5 м в вертикальной стенке закрытого резервуара закрыто щитом, вращающимся вокруг горизонтальной оси О и прижимаемым посредством двух грузов, подвешенных на рычагах r = 0,3 м. Определить минимально необходимый вес каждого груза, если глубина погружения нижней кромки отверстия Н = 0,6 м, а расстояние от верхней кромки отверстия до оси щита а = 30 мм. Весом рычагов и трением в подшипниках пренебречь.
Решение (pdf) Решение (docx)Задача 2.48
Цена - 130 руб. (pdf) - 160 руб. (word)
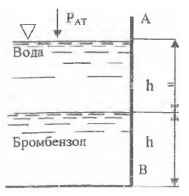
Определить величину и точку приложения суммарной силы давления воды и бромБензола на стенку АВ, ширина которой b = 1,6 м; γБ = 1500 кГ/м3; h1 = 1 м.
Решение (pdf) Решение (docx)Задача 2.49
Цена - 130 руб. (pdf) - 160 руб. (word)
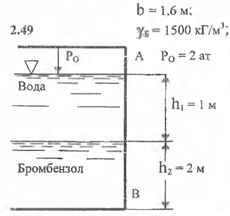
Определить величину и точку приложения суммарной силы давления воды и бромБензола на стенку АВ, ширина которой b = 1,6 м, γБ = 1500 кГ/м3; РO = 2 ат; h1 = 1 м, h2 = 2 м.
Решение (pdf) Решение (docx)Задача 2.50
Цена - 130 руб. (pdf) - 160 руб. (word)
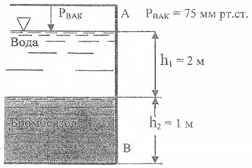
Определить величину и точку приложения суммарной силы давления воды и бромБензола на стенку АВ, ширина которой b = 1,6 м, Рвак = 75 мм.рт.ст; γБ = 1500 кГ/м3; h1 = 2 м, h2 = 1 м.
Решение (pdf) Решение (docx)Задача 2.51
Цена - 130 руб. (pdf) - 160 руб. (word)
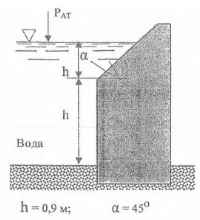
Определить величину и точку приложения суммарной силы гидростатического давления воды и ила на один погонный метр длины стенки, показанной на рисунке.
Решение (pdf) Решение (docx)Задача 2.53
Цена - 130 руб. (pdf) - 160 руб. (word)
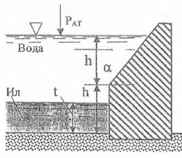
Определить величину и точку приложения суммарной силы гидростатического давления воды и ила на один погонный метр длины стенки, показанной на рисунке.
Решение (pdf) Решение (docx)Задача 2.54
Цена - 130 руб. (pdf) - 160 руб. (word)
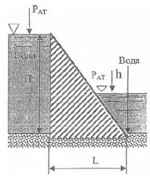
Вычислить коэффициент устойчивости Куст плотины против опрокидывания, который равен отношению Муд/Мопр, где Муд – момент, препятствующий опрокидыванию, Мопр − момент, опрокидывающий плотину. Н = 4,5 м; h = 1,5 м; L = 2,4 м; γБ = 2500 кГ/см3.
Решение (pdf) Решение (docx)Задача 2.55
Цена - 130 руб. (pdf) - 160 руб. (word)
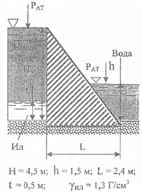
Вычислить коэффициент устойчивости Куст плотины против опрокидывания, который равен отношению Муд/Мопр, где Муд – момент, препятствующий опрокидыванию, Мопр − момент, опрокидывающий плотину. Н = 4,5 м; h = 1,5 м; L = 2,4 м; t = 0,5 м; γил = 1,3 Г/см3.
Решение (pdf) Решение (docx)Задача 2.56
Цена - 130 руб. (pdf) - 160 руб. (word)
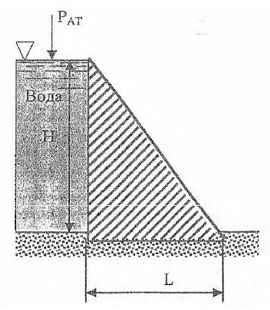
Вычислить коэффициент устойчивости Куст плотины против опрокидывания, который равен отношению моментов Муд/Мопр, где Муд – момент, препятствующий опрокидыванию, Мопр − момент, опрокидывающий плотину. Н = 4,5 м; h = 1,5 м; L = 2,4 м; t = 0,5 м; , 𝛾Б = 2500 кГ/см3.
Решение (pdf) Решение (docx)Задача 2.57
Цена - 130 руб. (pdf) - 160 руб. (word)
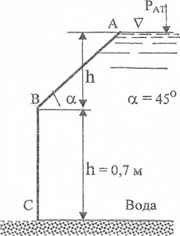
Определить величину и точку приложения суммарной силы гидростатического давления воды и ила на стенку АВС, шириной b = 1,2 м.
Решение (pdf) Решение (docx)Задача 2.58
Цена - 130 руб. (pdf) - 160 руб. (word)
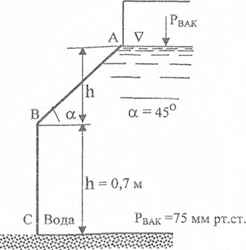
Определить величину и точку приложения суммарной силы гидростатического давления воды и ила на стенку АВС, шириной b = 1,2 м.
Решение (pdf) Решение (docx)Задача 2.59
Цена - 130 руб. (pdf) - 160 руб. (word)
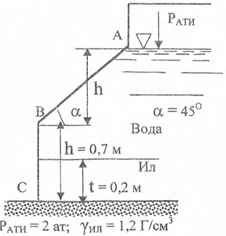
Определить величину и точку приложения суммарной силы гидростатического давления воды и ила на стенку АВС, шириной b = 1,2 м.
Решение (pdf) Решение (docx)Задача 2.60
Цена - 130 руб. (pdf) - 160 руб. (word)
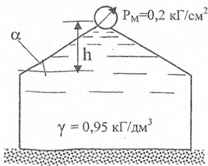
Определить суммарную силу, стремящуюся оторвать двухскатную крышу резервуара от его стенок. Длина резервуара L = 2 м; h = 0,45 м; α = 30 °.
Решение (pdf) Решение (docx)Задача 2.61
Цена - 130 руб. (pdf) - 160 руб. (word)
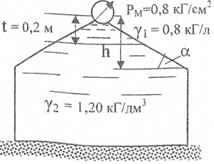
Определить суммарную силу, стремящуюся оторвать двухскатную крышу резервуара от его стенок. Длина резервуара L = 2 м; h = 0,45 м; α = 30 °.
Решение (pdf) Решение (docx)Задача 2.62
Цена - 130 руб. (pdf) - 160 руб. (word)
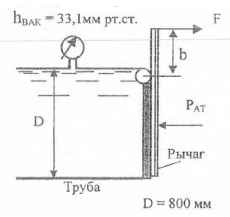
Определите усилие F, удерживающее клапан ОА от поворота вокруг шарнира О. b = 40 мм. Вакууметр показывает вакуумметрическую высоту hвак = 33,1 мм.рт.ст; D = 800 мм.
Решение (pdf) Решение (docx)Задача 2.63
Цена - 130 руб. (pdf) - 160 руб. (word)
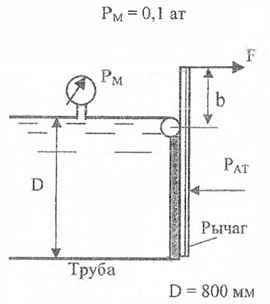
Определите усилие F, удерживающее клапан ОА от поворота вокруг шарнира О. b = 40 мм. Pм = 0,1 ат; D = 800 мм.
Решение (pdf) Решение (docx)Задача 2.64
Цена - 130 руб. (pdf) - 160 руб. (word)
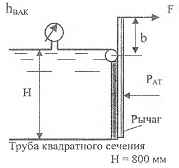
Определите усилие F, удерживающее клапан ОА от поворота вокруг шарнира О. b = 40 мм. Вакууметр показывает вакуумметрическую высоту hвак = 33,1 мм.рт.ст; H = 800 мм.
Решение (pdf) Решение (docx)Задача 2.65
Цена - 130 руб. (pdf) - 160 руб. (word)
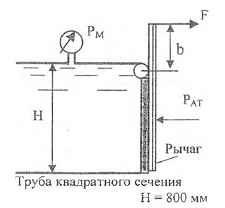
Определите усилие F, удерживающее клапан ОА от поворота вокруг шарнира О. b = 40 мм. Рм = 1,0 ат; H = 800 мм.
Решение (pdf) Решение (docx)Задача 2.66
Цена - 130 руб. (pdf) - 160 руб. (word)
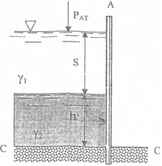
Щит АБ заделан нижним концом в бетон. Определить удельный вес γ1 и толщину S слоя жидкости, при которых максимальный изгибающий стойку момент в сечении С-С не будет превышать 3716 кГм, а избыточное давление на дне перед щитом не превысит РO = 0,25 кГ/см2. Ширина щита b = 1,7 м, h = 1,5 м, γ2 = 1,1 кГ/л.
Решение (pdf) Решение (docx)Задача 2.67
Цена - 130 руб. (pdf) - 160 руб. (word)
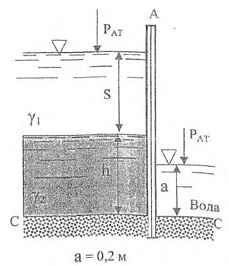
Щит АБ заделан нижним концом в бетон. Определить удельный вес γ1 и толщину S слоя жидкости, при которых максимальный изгибающий стойку момент в сечении С-С не будет превышать 3716 кГм, а избыточное давление на дне перед щитом не превысит РO = 0,25 кГ/см2. Ширина щита b = 1,7 м, h = 1,5 м, γ2 = 1,1 кГ/л; a = 0,2 м.
Решение (pdf) Решение (docx)Задача 2.68
Цена - 130 руб. (pdf) - 160 руб. (word)
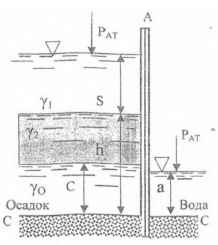
Щит АБ заделан нижним концом в бетон. Определить удельный вес γ1 и толщину S слоя жидкости, при которых максимальный изгибающий стойку момент в сечении С-С не будет превышать 3716 кГм, а избыточное давление на дне перед щитом не превысит РO = 0,25 кГ/см2. Ширина щита b = 1,7 м, h = 1,5 м, γ2 = 1,1 кГ/л; a = 0,2 м; С = 0,3 м; γ0 = 1,2 Г/см3.
Решение (pdf) Решение (docx)Задача 2.69
Цена - 130 руб. (pdf) - 160 руб. (word)
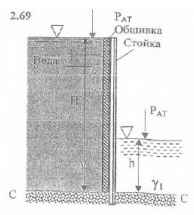
Стойка, заделанная нижним концом в бетон, воспринимает давление воды и некоторой жидкости, приходящееся на вертикальную полосу обшивки шириной b = 0,8 м и высотой Н = 2,4 м. Определить глубину h и удельный вес γ1 жидкости, при которых максимальный изгибающий стойку момент (в сечении С-С) не превысит 1660 кГм. Разность давлений по обе стороны стойки на уровне С-С не должна превышать 0,144 кГ/см2.
Решение (pdf) Решение (docx)Задача 2.70
Цена - 130 руб. (pdf) - 160 руб. (word)
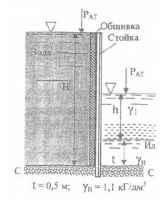
Стойка, заделанная нижним концом в бетон, воспринимает давление воды и некоторой жидкости, приходящееся на вертикальную полосу обшивки шириной b = 0,8 м и высотой Н = 2,4 м. Определить глубину h и удельный вес γ1 жидкости, при которых максимальный изгибающий стойку момент (в сечении С-С) не превысит 1660 кГм. Разность давлений по обе стороны стойки на уровне С-С не должна превышать 0,144 кГ/см2. t = 0,5 м; γи = 1,1 кГ/дм3.
Решение (pdf) Решение (docx)Задача 2.71
Цена - 130 руб. (pdf) - 160 руб. (word)
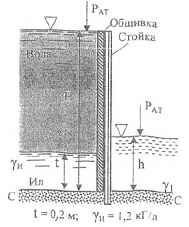
Стойка, заделанная нижним концом в бетон, воспринимает давление воды и некоторой жидкости, приходящееся на вертикальную полосу обшивки шириной b = 0,8 м и высотой Н = 2,4 м. Определить глубину h и удельный вес γ1 жидкости, при которых максимальный изгибающий стойку момент (в сечении С-С) не превысит 1660 кГм. Разность давлений по обе стороны стойки на уровне С-С не должна превышать 0,144 кГ/см2. t = 0,2 м; γи = 1,2 кГ/дм3.
Решение (pdf) Решение (docx)Задача 2.72
Цена - 130 руб. (pdf) - 160 руб. (word)
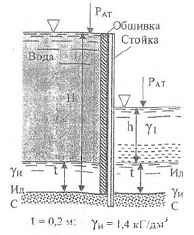
Стойка, заделанная нижним концом в бетон, воспринимает давление воды и некоторой жидкости, приходящееся на вертикальную полосу обшивки шириной b = 0,8 м и высотой Н = 2,4 м. Определить глубину h и удельный вес γ1 жидкости, при которых максимальный изгибающий стойку момент (в сечении С-С) не превысит 1660 кГм. Разность давлений по обе стороны стойки на уровне С-С не должна превышать 0,144 кГ/см2. t = 0,5 м; γи = 1,4 кГ/дм3.
Решение (pdf) Решение (docx)Задача 2.73
Цена - 130 руб. (pdf) - 160 руб. (word)
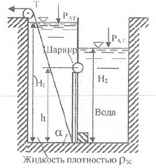
В перегородке, разделяющей резервуар на две части, имеется прямоугольное отверстие, которое закрывается поворотным щитом высотой h = 0,8 м и шириной b = 1,2 м. Определить, какую силу нужно приложить к тросу для поворота щита при следующих условиях: Н1 = 4,8 м; Н2 = 2,6 м; ∠α = 75 º; ρж = 0,8 т/м3. Найти также реакцию донного порога.
Решение (pdf) Решение (docx)Задача 2.74
Цена - 130 руб. (pdf) - 160 руб. (word)
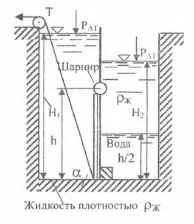
В перегородке, разделяющей резервуар на две части, имеется прямоугольное отверстие, которое закрывается поворотным щитом высотой h = 0,8 м и шириной b = 1,2 м. Определить, какую силу нужно приложить к тросу для поворота щита при следующих условиях: Н1 = 4,8 м; Н2 = 2,6 м; ∠α = 75 º; ρж = 0,8 т/м3. Найти также реакцию донного порога.
Решение (pdf) Решение (docx)Задача 2.75
Цена - 130 руб. (pdf) - 160 руб. (word)
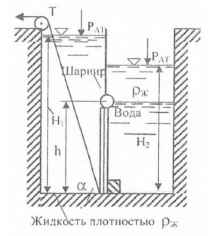
В перегородке, разделяющей резервуар на две части, имеется прямоугольное отверстие, которое закрывается поворотным щитом высотой h = 0,8 м и шириной b = 1,2 м. Определить, какую силу нужно приложить к тросу для поворота щита при следующих условиях: Н1 = 4,8 м; Н2 = 2,6 м; ∠α = 75 º; ρж = 0,8 т/м3. Найти также реакцию донного порога.
Решение (pdf) Решение (docx)Задача 2.76
Цена - 130 руб. (pdf) - 160 руб. (word)
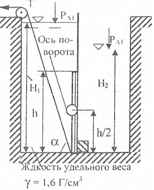
На рисунках изображен резервуар, предназначенный для приготовления раствора определенной концентрации. В перегородке, разделяющей резервуар на две камеры, имеется прямоугольное отверстие, которое закрывается поворотным щитом высотой h = 0,8 м и шириной b = 0,5 м. Определить, какую силу Т нужно приложить к тяге, чтобы щит прикрывался, когда удельный вес раствора в правой камере станет равным γ1 = 1,3 Т/м3 при следующих условиях: Н1 = 1,8 м; ∠α = 60 º; Н2 = 1,6 м (раствора). В правой камере первоначально находилась вода. В левой камере находится жидкость удельного веса γ = 1,6 Г/см3, уровень которой в процессе приготовления раствора остается неизменным.
Решение (pdf) Решение (docx)Задача 2.77
Цена - 130 руб. (pdf) - 160 руб. (word)
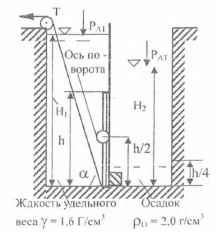
На рисунках изображен резервуар, предназначенный для приготовления раствора определенной концентрации. В перегородке, разделяющей резервуар на две камеры, имеется прямоугольное отверстие, которое закрывается поворотным щитом высотой h = 0,8 м и шириной b = 0,5 м. Определить, какую силу Т нужно приложить к тяге, чтобы щит прикрывался, когда удельный вес раствора в правой камере станет равным γ1 = 1,3 Т/м3 при следующих условиях: Н1 = 1,8 м; ∠α = 60 º; Н2 = 1,6 м (раствора). В правой камере первоначально находилась вода. В левой камере находится жидкость удельного веса γ = 1,6 Г/см3, уровень которой в процессе приготовления раствора остается неизменным.
Решение (pdf) Решение (docx)Задача 2.78
Цена - 130 руб. (pdf) - 160 руб. (word)
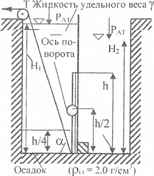
На рисунках изображен резервуар, предназначенный для приготовления раствора определенной концентрации. В перегородке, разделяющей резервуар на две камеры, имеется прямоугольное отверстие, которое закрывается поворотным щитом высотой h = 0,8 м и шириной b = 0,5 м. Определить, какую силу Т нужно приложить к тяге, чтобы щит прикрывался, когда удельный вес раствора в правой камере станет равным γ1 = 1,3 Т/м3 при следующих условиях: Н1 = 1,8 м; ∠α = 60 º; Н2 = 1,6 м (раствора). В правой камере первоначально находилась вода. В левой камере находится жидкость удельного веса γ = 1,6 Г/см3, уровень которой в процессе приготовления раствора остается неизменным.
Решение (pdf) Решение (docx)Задача 2.79
Цена - 130 руб. (pdf) - 160 руб. (word)
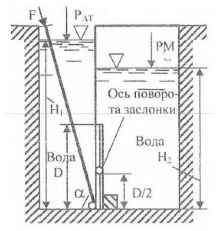
В перегородке, разделяющей резервуар на две части, имеется круглое отверстие, которое закрывается поворотной заслонкой диаметром D = 1,2 м. Определить, какую силу F нужно приложить к стержню T, чтобы заслонка не открывалась? При решении задачи необходимо учесть следующие исходные данные: Н1 = 4 м; Н2 = 2,6 м; D = 0,8 м; ∠α = 75 º; Рм = 4 кГ/см2.
Решение (pdf) Решение (docx)Задача 2.80
Цена - 130 руб. (pdf) - 160 руб. (word)
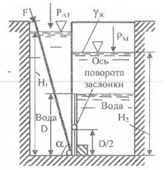
В перегородке, разделяющей резервуар на две части, имеется круглое отверстие, которое закрывается поворотной заслонкой диаметром D = 1,2 м. Определить, какую силу F нужно приложить к стержню T, чтобы заслонка не открывалась? При решении задачи необходимо учесть следующие исходные данные: Н1 = 4 м; Н2 = 2,6 м; D = 0,8 м; ∠α = 75 º; γж = 0,8 Г/см3; Рм = 2,0 ати.
Решение (pdf) Решение (docx)Задача 2.82
Цена - 130 руб. (pdf) - 160 руб. (word)
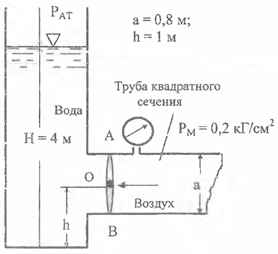
Определить величину и точку приложения равнодействующих сил давления воды и воздуха, действующих на затвор АВ. Н = 4 м; а = 0,8 м; h = 1 м; Рм = 0,2 кГ/см2.
Решение (pdf) Решение (docx)Задача 2.83
Цена - 130 руб. (pdf) - 160 руб. (word)
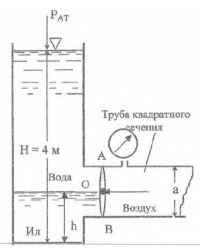
Определить величину и точку приложения равнодействующих сил давления воды и воздуха, действующих на затвор АВ. Н = 4 м; а = 0,8 м; h = 1 м; Рм = 0,2 кГ/см2; ρил = 1500 кг/м3.
Решение (pdf) Решение (docx)Задача 2.84
Цена - 130 руб. (pdf) - 160 руб. (word)
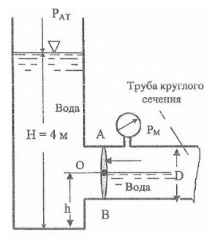
Определить величину и точку приложения равнодействующих сил давления воды и воздуха, действующих на затвор АВ. Н = 4 м; D = 0,8 м; а = 0,8 м; h = 1 м; Рм = 0,2 кГ/см2;
Решение (pdf) Решение (docx)Задача 2.85
Цена - 130 руб. (pdf) - 160 руб. (word)
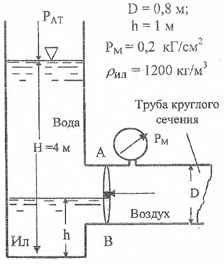
Определить величину и точку приложения равнодействующих сил давления воды и воздуха, действующих на затвор АВ. Н = 4 м; D = 0,8 м; а = 0,8 м; h = 1 м; Рм = 0,2 кГ/см2; ρил = 1500 кг/м3.
Решение (pdf) Решение (docx)Задача 2.86
Цена - 130 руб. (pdf) - 160 руб. (word)
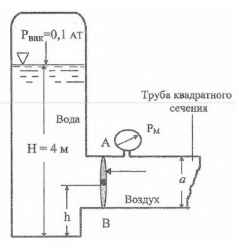
Определить величину и точку приложения равнодействующих сил давления воды и воздуха, действующих на затвор АВ. РВАК = 0,1 АТ; Н = 4 м; а = 0,8 м; h = 1 м; Рм = 0,2 кГ/см2;
Решение (pdf) Решение (docx)Задача 2.87
Цена - 130 руб. (pdf) - 160 руб. (word)
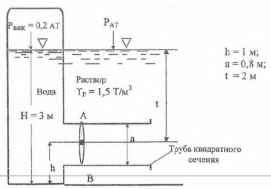
Определить величину и точку приложения равнодействующей сил давления воды и раствора на затвор АВ. Н = 3 м; а = 0,8 м; h = 1 м; Рвак = 0,2 ат; γр = 1,5 Т/м3.
Решение (pdf) Решение (docx)Задача 2.88
Цена - 130 руб. (pdf) - 160 руб. (word)
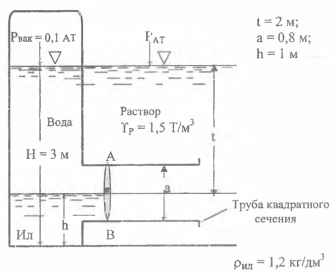
Определить величину и точку приложения равнодействующей сил давления воды и раствора на затвор АВ. Н = 3 м; t = 2 м; а = 0,8 м; h = 1 м; Рвак = 0,1 ат; γр = 1,5 Т/м3; γил = 1,2 кг/дм3.
Решение (pdf) Решение (docx)Задача 2.89
Цена - 130 руб. (pdf) - 160 руб. (word)
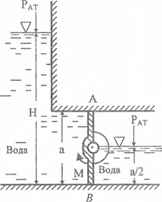
Определите момент М, необходимый для открывания затвора АВ, имеющего форму прямоугольника шириной b = 0,6 м. Н = 3,2 м; а = 0,9 м.
Решение (pdf) Решение (docx)Задача 2.90
Цена - 130 руб. (pdf) - 160 руб. (word)
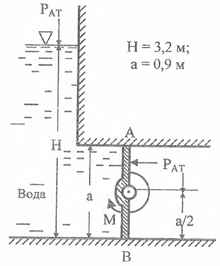
Определите момент М, необходимый для открывания затвора АВ, имеющего форму прямоугольника шириной b = 0,6 м. Н = 3,2 м; а = 0,9 м.
Решение (pdf) Решение (docx)Задача 2.92
Цена - 130 руб. (pdf) - 160 руб. (word)
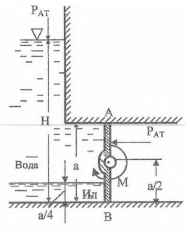
Определите момент М, необходимый для открывания затвора АВ, имеющего форму прямоугольника шириной b = 0,6 м. Н = 3,2 м; а = 0,9 м; ρил = 1,2 г/см3.
Решение (pdf) Решение (docx)Задача 2.94
Цена - 130 руб. (pdf) - 160 руб. (word)
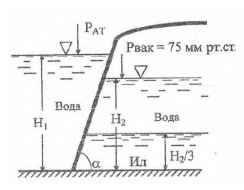
Определить давление на один погонный метр ширины наклонной стенки, а также точку приложения равнодействующей, если известны: Н1 = 2,0 м, Н2 = 1,0 м, угол наклона стенки к горизонту α = 60 °. PВАК = 75 мм.рт.ст; ρил = 2,0 кг/дм3.
Решение (pdf) Решение (docx)Задача 2.95
Цена - 130 руб. (pdf) - 160 руб. (word)
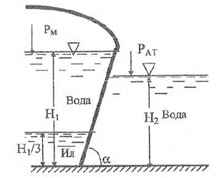
Определить давление на один погонный метр ширины наклонной стенки, а также точку приложения равнодействующей, если известны: Н1 = 2,0 м, Н2 = 1,0 м, угол наклона стенки к горизонту α = 60 °. Pм = 0,1 атм; ρил = 1,2 кг/дм3.
Решение (pdf) Решение (docx)Задача 2.96
Цена - 130 руб. (pdf) - 160 руб. (word)
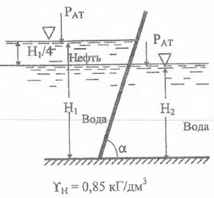
Определить давление на один погонный метр ширины наклонной стенки, а также точку приложения равнодействующей, если известны: Н1 = 2,0 м, Н2 = 1,0 м, угол наклона стенки к горизонту α = 60 °. γH = 0,85 кГ/дм3.
Решение (pdf) Решение (docx)Задача 2.97
Цена - 130 руб. (pdf) - 160 руб. (word)
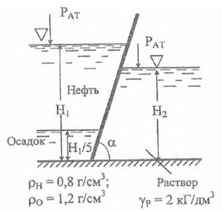
Определить давление на один погонный метр ширины наклонной стенки, а также точку приложения равнодействующей, если известны: Н1 = 2,0 м, Н2 = 1,0 м, угол наклона стенки к горизонту α = 60 °. ρH = 0,8 г/см3; ρО = 1,2 г/см3; Раствор γР = 2 кГ/дм3.
Решение (pdf) Решение (docx)Задача 2.98
Цена - 130 руб. (pdf) - 160 руб. (word)
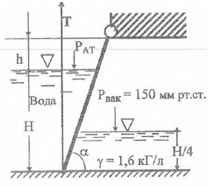
Определить усилие Т, необходимое для подъема щита шириной b = 1 м, пренебрегая его весом и трением в шарнире, если известно: Н = 1,6 м; h = 0,4 м; α = 60 °. PВАК = 150 мм.рт.ст.
Решение (pdf) Решение (docx)Задача 2.99
Цена - 130 руб. (pdf) - 160 руб. (word)
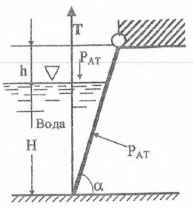
Определить усилие Т, необходимое для подъема щита шириной b = 1 м, пренебрегая его весом и трением в шарнире, если известно: Н = 1,6 м; h = 0,4 м; α = 60 °.
Решение (pdf) Решение (docx)Задача 2.100
Цена - 130 руб. (pdf) - 160 руб. (word)
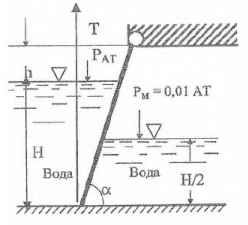
Определить усилие Т, необходимое для подъема щита шириной b = 1 м, пренебрегая его весом и трением в шарнире, если известно: Н = 1,6 м; h = 0,4 м; α = 60 °. РМ = 0,1 АТ.
Решение (pdf) Решение (docx)Задача 2.101
Цена - 130 руб. (pdf) - 160 руб. (word)
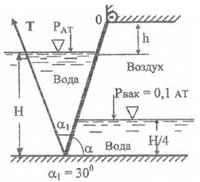
Определить усилие Т, необходимое для подъема щита шириной b = 1 м, пренебрегая его весом и трением в шарнире, если известно: Н = 1,6 м; h = 0,4 м; α = 60 °. РВАК = 0,1 АТ; α1 = 30 °.
Решение (pdf) Решение (docx)Задача 2.105
Цена - 130 руб. (pdf) - 160 руб. (word)
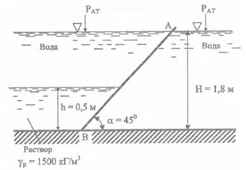
Определить величину и точку приложения суммарной силы давление воды и раствора на стенку АВ, ширина которой b = 2,4 м.
Решение (pdf) Решение (docx)Задача 2.106
Цена - 130 руб. (pdf) - 160 руб. (word)
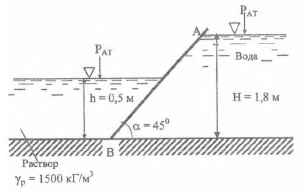
Определить величину и точку приложения суммарной силы давление воды и раствора на стенку АВ, ширина которой b = 2,4 м.
Решение (pdf) Решение (docx)Задача 2.107
Цена - 130 руб. (pdf) - 160 руб. (word)
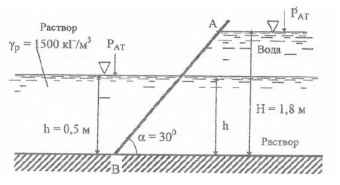
Определить величину и точку приложения суммарной силы давление воды и раствора на стенку АВ, ширина которой b = 2,4 м.
Решение (pdf) Решение (docx)Задача 2.108
Цена - 130 руб. (pdf) - 160 руб. (word)
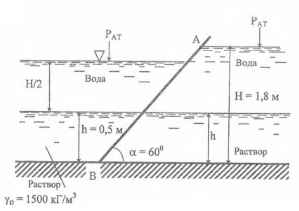
Определить величину и точку приложения суммарной силы давление воды и раствора на стенку АВ, ширина которой b = 2,4 м.
Решение (pdf) Решение (docx)Задача 2.109
Цена - 130 руб. (pdf) - 160 руб. (word)
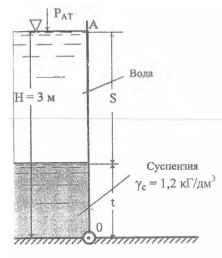
Требуется определить толщины слоев воды S и суспензии t при которых сумма моментов сил давления воды и суспензии на щит АО относительно шарнира О будет равна М = 900 кГм. Суммарная толщина слоев жидкостей должна составлять Н = 3 м. Ширина щита b = 1 м.
Решение (pdf) Решение (docx)Задача 2.110
Цена - 130 руб. (pdf) - 160 руб. (word)
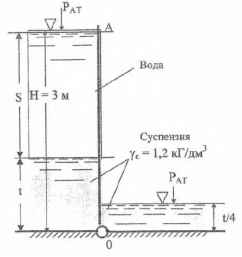
Требуется определить толщины слоев воды S и суспензии t при которых сумма моментов сил давления воды и суспензии на щит АО относительно шарнира О будет равна М = 900 кГм. Суммарная толщина слоев жидкостей должна составлять Н = 3 м. Ширина щита b = 1 м.
Решение (pdf) Решение (docx)Задача 2.111
Цена - 130 руб. (pdf) - 160 руб. (word)
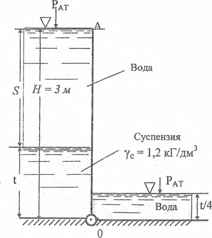
Требуется определить толщины слоев воды S и суспензии t при которых сумма моментов сил давления воды и суспензии на щит АО относительно шарнира О будет равна М = 900 кГм. Суммарная толщина слоев жидкостей должна составлять Н = 3 м. Ширина щита b = 1 м.
Решение (pdf) Решение (docx)Задача 2.113
Цена - 130 руб. (pdf) - 160 руб. (word)
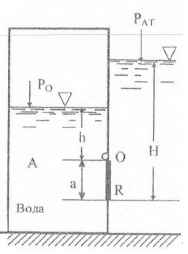
Степень наполнения резервуара А водой и давление на ее свободной поверхности регулируется щитком OR, поворачивающимся вокруг шарнира О. Определить давление РO, при котором прямоугольное отверстие (шириной b = 0,6 м) в стенке резервуара будет перекрыто щитком OR.
Решение (pdf) Решение (docx)Задача 2.115
Цена - 130 руб. (pdf) - 160 руб. (word)
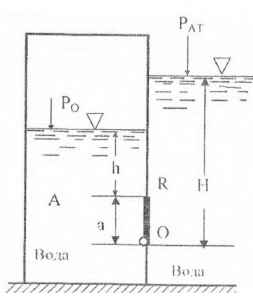
Степень наполнения резервуара А водой и давление на ее свободной поверхности регулируется щитком OR, поворачивающимся вокруг шарнира О. Определить давление РO, при котором прямоугольное отверстие (шириной b = 0,6 м) в стенке резервуара будет перекрыто щитком OR.
Решение (pdf) Решение (docx)Задача 2.117
Цена - 130 руб. (pdf) - 160 руб. (word)
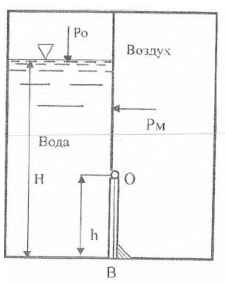
Определить давление РO при котором силы давления на квадратный щиток ОВ воды (слева) и воздуха (справа) будут одинаковы по величине. Чему при этом будет равна сумма моментов этих сил относительно шарнира О? Н = 2,2 м; Рм = 0,1 кГ/см2; h = 0,6 м.
Решение (pdf) Решение (docx)Задача 2.121
Цена - 130 руб. (pdf) - 160 руб. (word)
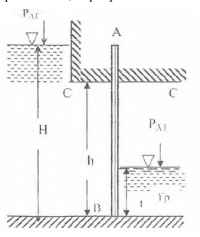
Щит АВ, заделанный верхним краем в бетон, перекрывает отверстие высотой h = 1,2 м и шириной b = 1 м. Перед щитом находится вода, за щитом – раствор. Требуется определить: 1) толщину слоя t раствора, при которой изгибающий момент в сечении С – С’ будет равен нулю; 2) чему при этом будет равна сила, перерезывающая щит в сечении С – С?
Исходные данные: γр = 2,0 кГ/дм3; Н = 2 м; h = 1,2 м.
Задача 2.126
Цена - 130 руб. (pdf) - 160 руб. (word)
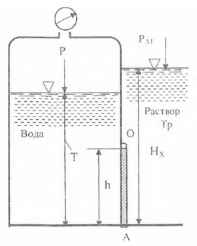
Требуется определить: 1) высоту столба Нх раствора, при которой моменты сил давления на щит ОА воды и раствора относительно шарнира О будут одинаковы по относительной величине; 2) чему при этом будут равны силы давления и раствора. Ширина щита ОА b = 1 м; Р = 0,08 кГ/см2; Т = 1,6 м; h = 0,8 м; γр = 1,6 кГ/дм3.
Решение (pdf) Решение (docx)Задача 2.132
Цена - 130 руб. (pdf) - 160 руб. (word)
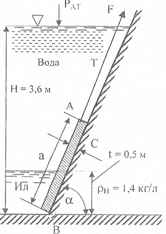
Определить начальное усилие F, которое нужно приложить к тросу Т, чтобы поднять щит АВ по наклонной плоскости с углом наклона к горизонту α = 60 °. Щит имеет форму параллелепипеда с размерами a x b x c = 2 х 1,6 х 0,25 м и изготовлен из материала, с удельным весом γМ = 1,5 Т/м3. Коэффициент трения щита о наклонную плоскость f = 0,3.
Решение (pdf) Решение (docx)Задача 2.172
Цена - 130 руб. (pdf) - 160 руб. (word)
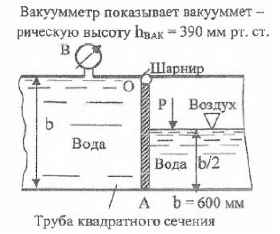
Требуется определить давление воздуха, при котором труба будет перекрыта клапаном ОА. Вакуумметр показывает вакуумметрическую высоту hвак = 390 мм рт. ст.
Решение (pdf) Решение (docx)Задача 2.173
Цена - 130 руб. (pdf) - 160 руб. (word)
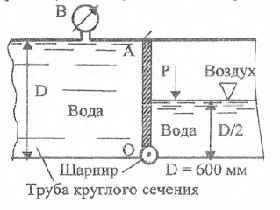
Требуется определить давление воздуха, при котором труба будет перекрыта клапаном ОА. Вакуумметр показывает вакуумметрическую высоту hвак = 75 мм рт. ст.
Решение (pdf) Решение (docx)Задача 2.195
Цена - 130 руб. (pdf) - 160 руб. (word)
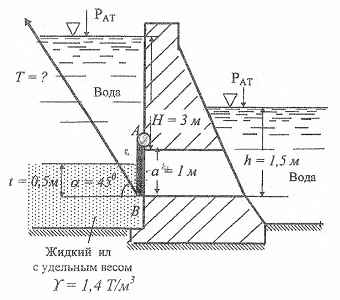
Определить с какой силой Т нужно потянуть за трос, чтобы открыть щит АВ, ширина щита b = 1,2 м.
Решение (pdf) Решение (docx)Задача 2.200
Цена - 130 руб. (pdf) - 160 руб. (word)
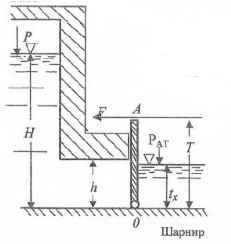
Определить глубину tх, при которой показанное на рисунке водопропускное отверстие будет перекрыто затвором ОА при приложении к нему силы F = 100 кГ. Ширина отверстия b = 0,75 м. Н = 3,0 м; h = 0,5 м; P = 0,2 ат; Т = 1,0 м.
Решение (pdf) Решение (docx)3. ОПРЕДЕЛЕНИЕ СУММАРНОЙ СИЛЫ ГИДРОСТАТИЧЕСКОГО ДАВЛЕНИЯ НА КРИВОЛИНЕЙНЫЕ ПОВЕРХНОСТИ
3.3. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Задачи: 3.1 - 3.52
Общее условие для Задач 3.1 - 3.52:
Цена Задачи - 150 руб. (Pdf) - 180 руб. (Word)
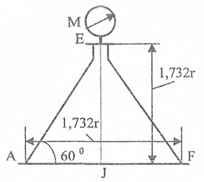
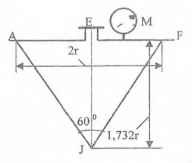
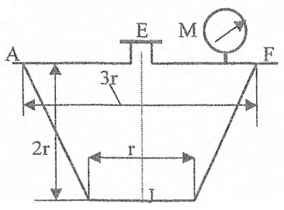
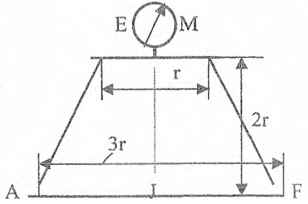
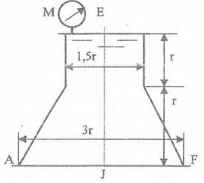
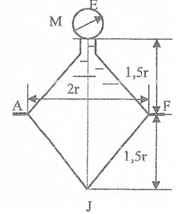
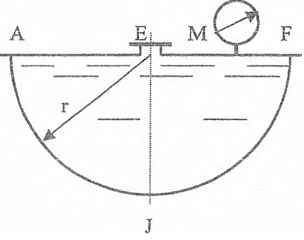
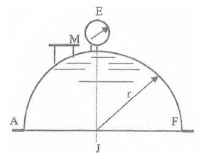
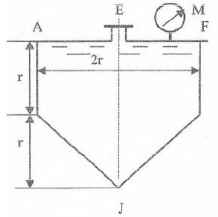
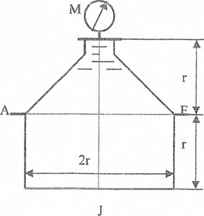
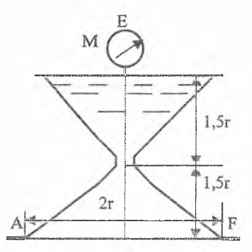
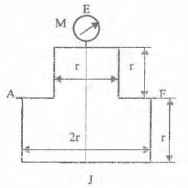
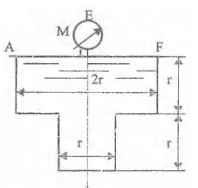
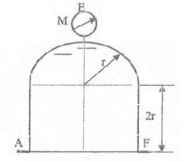
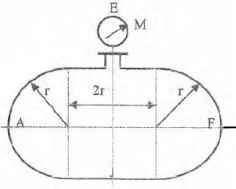
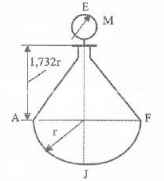
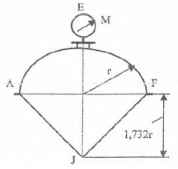
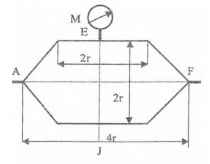
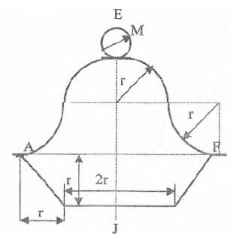
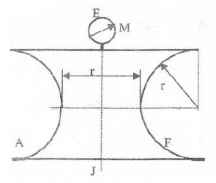
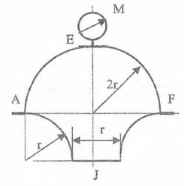
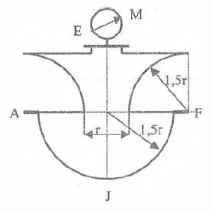
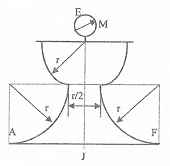
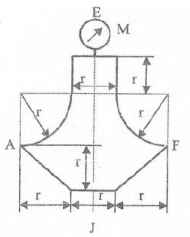
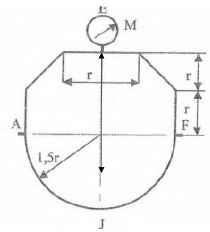
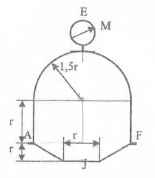
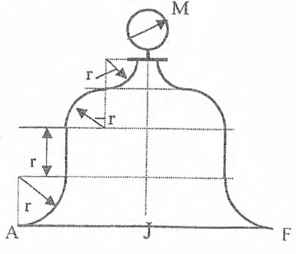
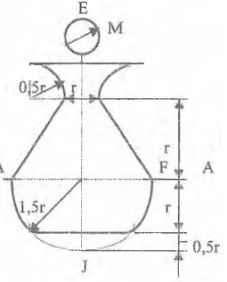
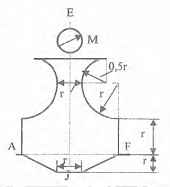
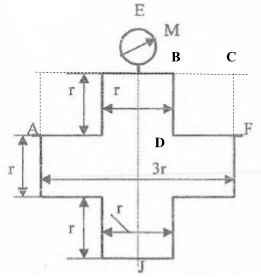
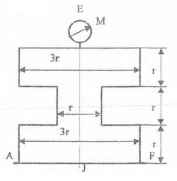
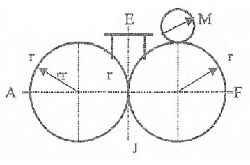
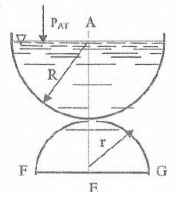
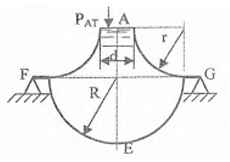
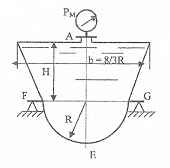
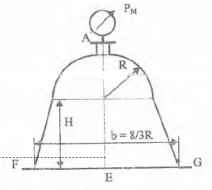
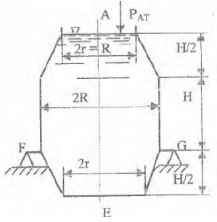
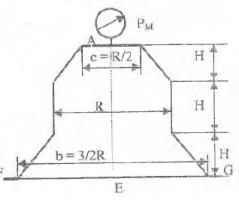
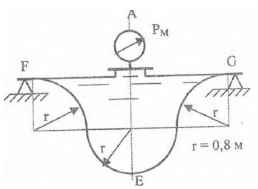
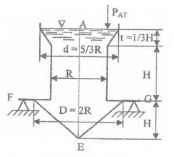
Оболочки резервуаров, предназначенных для хранения в них тяжелых жидкостей, имеют внешние очертания тел, образуемых вращением показанных на рисунках фигур вокруг их осей EJ. Род и плотность ρ, заполняющих резервуар жидкостей, задается преподавателем (см. табл.1 в Приложении). Для резервуара в задаче требуется определить силу, стремящуюся разорвать резервуар по сечению EJ, а также силу, стремящуюся оторвать верхнюю часть (или крышку) резервуара от его днища по шву AF.
Размер r = 0,9 м; показания манометра M Рм = 68,67 кПа.
Примечание. Силы Fx и Fz, стремящиеся разорвать резервуар по сечениям EJ и AF , численные значения которых приведены в ответах к задачам 3.1 - 3.24, возникают при заполнении резервуаров смолой, обладающей плотностью ρс = 1100 кг/м3; в ответах к задачам 3.25 - 3.48 приведены значения сил Fx и Fz, возникающих при заполнении рассматриваемых в этих задачах резервуаров бромБензолом, обладающимплотностью ρб = 1500 кг/м3. Численные значения сил Fx и Fz, возникающих при заполнении тех же резервуаров другими жидкостями, могут быть получены несложным пересчетом значений этих сил, приведенных в ответах.
Задачи: 3.1
Задача 3.53
Цена - 150 руб. (pdf) - 180 руб. (word)
Рассчитать толщину стенки стальной трубы, диаметром d = 0,4 м на внутреннее давление Р = 16 ат. Допустимое напряжение принять равным 800 кГ/см2.
Решение (pdf) Решение (docx)Задача 3.54
Цена - 150 руб. (pdf) - 180 руб. (word)
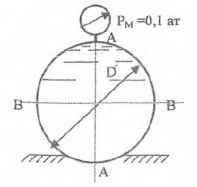
Определить силы, растягивающие горизонтальную цистерну, заполненную жидкостью удельного веса γ по сечениям А-А и Б-Б. Диаметр цистерны D = 5 м, ее длина L = 10 м. Жидкость – Масло Веретенное АУ, ρ = 880 кг/м3, γ = 8624 Н/м3.
Масло Веретенное АУ (pdf) Масло Веретенное АУ (docx)Задача 3.55
Цена - 150 руб. (pdf) - 180 руб. (word)
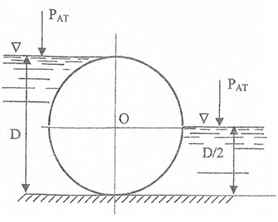
Цилиндрический затвор имеет диаметр D = 2 м и длину L = 5 м. Определить величину и направление силы F полного гидростатического давления жидкости.
Задача 3.56
Цена - 150 руб. (pdf) - 180 руб. (word)
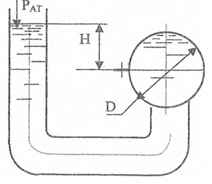
Определить силу F, действующую на болты шара диаметром D = 2 м, заполненного жидкостью. H = 10 м; Жидкость - Масло Сепараторное, ρ = 900 кг/м3; γ = 8830 Н/м3.
Решение (pdf) Решение (docx)Задача 3.58
Цена - 150 руб. (pdf) - 180 руб. (word)
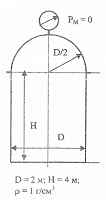
Определить силу Fz, отрывающую полусферу от цилиндра и силу Fх, разрывающую резервуар по образующей. Резервуар полностью заполнен жидкостью, значение которой приведено в соответствующей задаче.
Задача 3.60
Цена - 150 руб. (pdf) - 180 руб. (word)
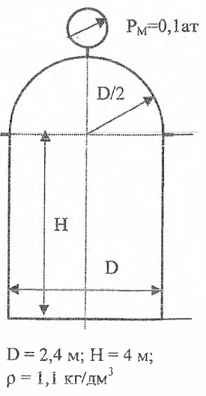
Определить силу Fz, отрывающую полусферу от цилиндра, и силу Fx, растягивающую резервуар по образующей. Резервуар полностью заполнен жидкостью с плотностью ρ, значение которой приведено в соответствующей задаче. D = 2,4 м; H = 4 м; Жидкость - Вазелиновое Масло, ρ = 870 кг/м3, γ = 8526 Н/м3.
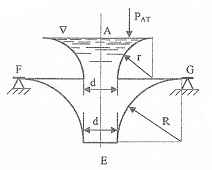
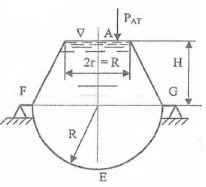
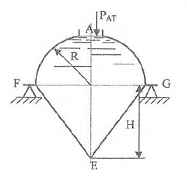
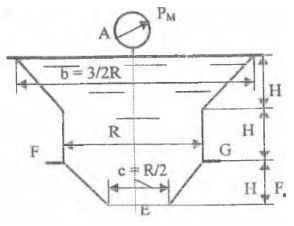
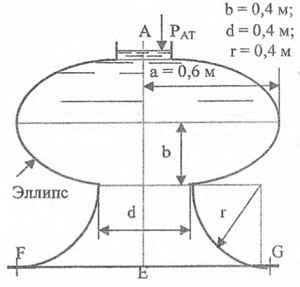
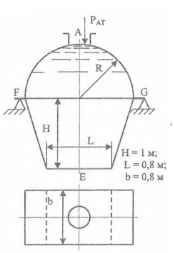
Решение (pdf) Решение (docx)Общее условие для Задач 3.61-3.111:
Цена Задачи - 150 руб. (Pdf) - 180 руб. (Word)
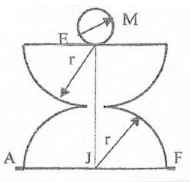
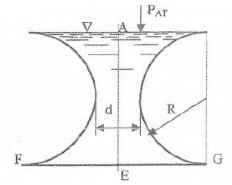
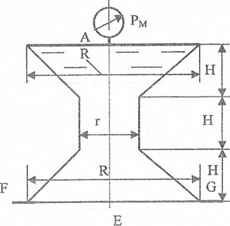
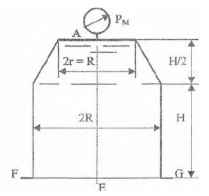
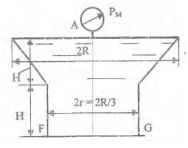
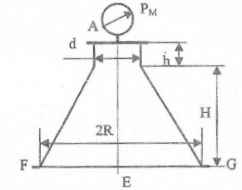
Резервуары, схемы которых приведены на рисунках, заполнены жидкостью (род жидкости в соответствующем резервуаре задается преподавателем, а её плотность ρ приведена в табл. 1 Приложения). Требуется определить силы, стремящиеся разорвать резервуар по сечениям АЕ и FG. Геометрические размеры: R = 1 м; r = 0,5 м; d = (R – r)/2; Н = 3 м; показание манометра Рм = 0,2 ати.
Задачи: 3.61
3.4. МНОГОВАРИАНТНЫЕ ЗАДАЧИ
Задача 3.4.2
Задача 1
Цена - 150 руб. (pdf) - 170 руб. (word)
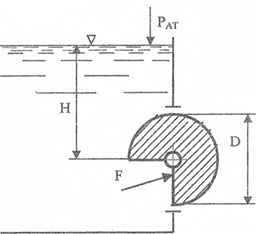
В прямоугольном окне вертикальной стенки резервуара установлен на цапфах цилиндрический затвор диаметром D и шириной b. Определить суммарное усилие на цапфы и момент сил от воздействия воды на затвор при напоре Н.
Задача 3.4.5
Цена - 150 руб. (pdf) - 170 руб. (word)
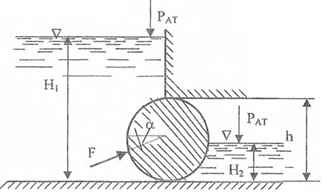
Определить величину и направление (угол α) равнодействующей силы F давления воды на цилиндрический затвор плотины, перекрывающей прямоугольное донное отверстие высотой h и шириной b. Глубина воды слева Н1 справа Н2.