
Задачник по ТЕПЛОМАССООБМЕНУ
Учебное пособие для направление подготовки 140100 "Теплоэнергетика". Москва 2008 г.
Ф.Ф.Цветков, Р.В.Керимов, В.И.Величко

ГЛАВА 1. СТАЦИОНАРНАЯ ТЕПЛОПРОВОДНОСТЬ
Задача 1.1
Цена - 100 руб. (pdf) - 120 руб. (word)
Плоская стенка выполнена из материала с коэффициентом теплопроводности λ = 20 Вт/(м · К). Толщина стенки δ = 10 мм. На одной стороне стенки температура tс1 = 100 °С, на другой 90 °С. Найти плотность теплового потока через стенку и температуру в середине стенки.
Решение (pdf) Решение (docx)Задача 1.2
Цена - 100 руб. (pdf) - 120 руб. (word)
В теплообменнике горячий и холодный теплоносители разделены плоской латунной стенкой [δ = 2 мм, λ = 100 Вт/(м·К)], перепад температур в которой tс1 – tс2 = 5 °C. Вычислить плотность теплового потока через стенку. Определить толщину стальной [λ = 45 Вт/(м · К]) и медной [λ = 370 Вт/(м · К)] стенок, чтобы при том же перепаде температур плотность теплового потока осталась неизменной.
Решение (pdf) Решение (docx)Задача 1.3
Цена - 100 руб. (pdf) - 120 руб. (word)
Чему равен тепловой поток через стену из красного кирпича высотой 4 м, шириной 5 м и толщиной 500 мм? На одной поверхности стены температура 19 °С, на другой 2 °С.
Решение (pdf) Решение (docx)Задача 1.13
Цена - 100 руб. (pdf) - 120 руб. (word)
Чтобы уменьшить до заданного значения тепловые потери с поверхности промышленного теплообменника, решили закупить тепловую изоляцию с λ′из = 0,2 Вт/(м ∙ К). Оказалось, что на складе имеется изоляция, для которой λиз″ = 0,1 Вт/(м ∙ К), но она на 50 % дороже первой. Больше или меньше (и насколько) придется заплатить за вторую изоляцию?
Решение (pdf) Решение (docx)Задача 1.17
Цена - 100 руб. (pdf) - 120 руб. (word)
Температура воздуха в аудитории tж1 = 19,5 °С, а внешнего воздуха tж2 = –18 °С. Вычислить тепловые потери из аудитории, если наружная стена (L = 8 м, H = 4,5 м, δ = 0,5 м, окон нет) из кирпичной кладки, а коэффициенты теплоотдачи к ее внутренней поверхности α1 = 5,8 Вт/(м2 ∙ К) и с ее внешней поверхности α2 = 15 Вт/(м2 ∙ К)
Решение (pdf) Решение (docx)Задача 1.23
Цена - 100 руб. (pdf) - 120 руб. (word)
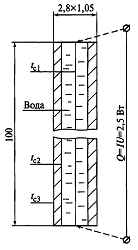
В приборе для определения коэффициента теплопроводности методом нагретой нити в кольцевом зазоре между платиновой нитью (d1 = 0,1 мм, l = 100 мм) и кварцевой трубкой [d2 × δ = 2,8 × 1,05 мм, λкв = 1,76 Вт/(м ∙ К)] находится вода (p = 20 ∙ 105 Па). Определить коэффициент теплопроводности и среднюю температуру воды в зазоре, если при тепловыделении в нити (путем пропускания электрического тока) Q = 2,5 Вт температура ее поверхности tс1 = 220 °С, а температура внешней поверхности кварцевой трубки tс3 = 204,9 °С (рис. 1.3).
Решение (pdf) Решение (docx)Задача 1.25
Цена - 100 руб. (pdf) - 120 руб. (word)
Стальной паропровод (d2 × δ = 110 × 5 мм) проложен на открытом воздухе tж2 = 20 °С. Тепловая изоляция паропровода выполнена из двух слоев – минеральной стеклянной ваты и асбеста (ρ = 500 кг/м3) δм.в = δа = 50 мм). Вычислить потери тепла с 1 п. м (погонного метра) паропровода, если температура пара tж1 = 300 ℃, а коэффициенты теплоотдачи от пара к внутренней поверхности паропровода и с внешней поверхности второго слоя изоляции к воздуху равны соответственно 90 Вт/(м2∙К) и 15 Вт/(м2 ∙ К). Как изменятся полученные результаты, если при других одинаковых условиях внутренний и наружный слои изоляции поменять местами?
Решение (pdf) Решение (docx)Задача 1.27
Цена - 100 руб. (pdf) - 120 руб. (word)
По трем стальным трубам (d2 × δ = 100 × 3 мм, L = 200 м), расположенным на открытом воздухе (tж2 = 5 °С) горячая вода, подогретая в теплообменнике до 100 °С, транспортируется к потребителю со скоростью w = 0,25 м/с в каждой. С какой температурой будет получать воду потребитель, если первая труба покрыта слоем минеральной ваты [λ = 0,05 Вт/(м ∙ К), δ = 50 мм], вторая − слоем бетона [λб = 1,28 Вт/(м ∙ К), δ = 50 мм], а третья труба не изолирована. Коэффициент теплоотдачи от горячей воды к внутренней поверхности труб принять α1 = 300 Вт/(м2 ∙ К), а с внешней поверхности каждой из трех труб к окружающему воздуху − одинаковым: α2 =12,8 Вт/(м2 ∙ К).
Решение (pdf) Решение (docx)Задача 1.29
Цена - 100 руб. (pdf) - 120 руб. (word)
В трубчатом теплообменнике средняя температура жидкости tж1 = 200 °С, а tж2 = 100 °С. Коэффициенты теплоотдачи α1 = 2000 Вт/(м2 ∙ К), α2 = 100 Вт/(м2 ∙ К). Наружный диаметр латунных труб равен d2 = 20 мм, толщина стенки составляет δ = 1 мм. Найдите коэффициент теплопередачи k, среднюю плотность теплового потока q от горячей жидкости к холодной, а также tc1 и tc2.
Решение (pdf) Решение (docx)Задача 1.30
Цена - 100 руб. (pdf) - 120 руб. (word)
В зимний период тепловые потери через наружную стену аудитории составляют 1,5 кВт. Какой длины должны быть радиаторы отопления из стальных труб [d2 × δ = 50 × 3 мм, λ = 50,2 Вт/(м ∙ К)], если греющей средой служит вода при tж1 = 90 °С, а температура воздуха в аудитории tж2 = 20 °С? Принять коэффициенты теплоотдачи со стороны горячего и холодного теплоносителей 4000 и 9 Вт/(м2 ∙ К) соответственно. Как изменится полученный результат, если при всех других неизменных условиях радиаторы покрасить [δкр = 3 мм, λкр = 2 Вт/(м ∙ К)]? Какая температура воздуха установится в помещении, если покрасить радиаторы отопления исходной длины при неизменных значениях коэффициента теплопередачи через наружную стену и температурe наружного воздуха tж3 = –18 °С? Как изменятся результаты во всех случаях, если вместо стальных труб использовать медные [λ = 300 Вт/(м ∙ К)]?
Решение (pdf) Решение (docx)Задача 1.31
Цена - 100 руб. (pdf) - 120 руб. (word)
По электропроводу (d = 2 мм, Rlэл = 5,6 ∙ 10–3 Ом/м) пропускают ток I = 30 А. Определить температуру поверхности провода, если коэффициент теплоотдачи к окружающему воздуху (tж = 20 °С) составляет 12 Вт/(м2 ∙ К). Как изменится температура поверхности электропровода, если его покрыть резиновой изоляцией [λр = 0,16 Вт/(м ∙ К)] толщиной 1,5 мм при неизменных значениях тока, коэффициента теплоотдачи и температуры воздуха?
Решение (pdf) Решение (docx)Задача 1.32
Цена - 100 руб. (pdf) - 120 руб. (word)
Определить максимально допустимый ток по медному электропроводу (d = 2 мм, Rlэл = 5,6∙10–3 Ом/м), покрытому резиновой изоляцией [δ = 2 мм, λр = 0,18 Вт/(м∙К)], если температура ее внешней поверхности не должна превышать 60 °C. Принять коэффициент теплоотдачи 12 Вт/(м2∙К), а температуру окружающего воздуха 20 °С. Вычислить температуру на поверхности электропровода.
Решение (pdf) Решение (docx)Задача 1.33
Цена - 100 руб. (pdf) - 120 руб. (word)
По алюминиевому электропроводу (d = 4 мм, ρэл = 0,0281 Ом∙мм2/м) пропускают ток I = 100 А. Вычислить температуру его поверхности. Какой толщины должна быть изоляция из каучука [λк = 0,15 Вт/(м∙К)], если допустимая температура наружной ее поверхности tиз = 60 °С? Коэффициент теплоотдачи [α = 10 Вт/(м2∙К)] и температура окружающего воздуха (tж = 20 °С) в обоих случаях неизменны. Какой будет температура поверхности изолированного провода?
Решение (pdf) Решение (docx)Задача 1.34
Цена - 100 руб. (pdf) - 120 руб. (word)
Для уменьшения тепловых потерь на поверхность паропровода d2 = 30 мм решено наложить слой изоляции толщиной 20 мм. Какие из перечисленных теплоизоляционных материалов отвечают решению поставленной задачи: 1) глина огнеупорная [λг = 1,04 Вт/(м∙К)]; 2) пеношамот [λп = 0,28 Вт/(м∙К)]; 3) асбестовый шнур [λа.ш = 0,13 Вт/(м∙К)]; 4) асбослюда [λа.с = 0,12 Вт/(м∙К)]; 5) минеральная вата [λм.в = 0,05 Вт/(м∙К)]? Сравнить тепловые потери с 1 п.м оголенного и изолированного наиболее эффективным материалом паропровода при неизменных температуре поверхности паропровода (tс = 200 °С), температуре окружающего воздуха (tж = 20 °С) и коэффициенте теплоотдачи α = 8 Вт/(м2∙К).
Решение (pdf) Решение (docx)Задача 1.35
Цена - 100 руб. (pdf) - 120 руб. (word)
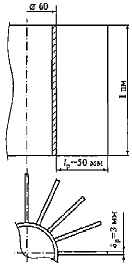
Для десятикратного увеличения теплового потока с 1 п.м. наружной поверхности вертикальной трубы (d = 60 мм, tс = 80 ℃) к воздуху в помещении (tж = 20 ℃) решено приварить к ней с равномерным шагом по периметру продольные стальные [λ = 50,1 Вт/(м ∙ К)] ребра прямоугольного сечения толщиной δ = 3 мм. Длина ребер l = 50 мм. Какое число ребер потребуется для этого, если коэффициент теплоотдачи с поверхности трубы и ребер 7,5 Вт/(м2 ∙ К)? Чему равен тепловой поток с гладкой части поверхности трубы между ребрами?
Решение (pdf) Решение (docx)Задача 1.36
Цена - 100 руб. (pdf) - 120 руб. (word)
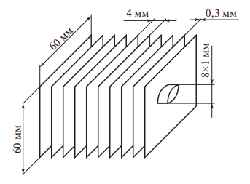
Конденсатор холодильной машины, обдуваемый воздухом, представляет собой змеевик из латунных труб (d2 × δ = 8 × 1 мм), на которые плотно насажены алюминиевые ребра − квадратные пластины толщиной δр = 0,3 мм и стороной b = 60 мм. Центр квадрата совпадает с осью трубы; шаг между ребрами 4 мм. Температура хладагента в конденсаторе tж1 = 35 °С; температура воздуха tж2 = 20 °С. Коэффициент теплоотдачи к воздуху α2 = 50 Вт/(м2∙К), а теплоотдача от хладагента α1 >> α2. Рассчитать длину труб конденсатора, необходимую для отвода Q = 3,5 кВт (рис. 1.5).
Решение (pdf) Решение (docx)Задача 1.37
Цена - 100 руб. (pdf) - 120 руб. (word)
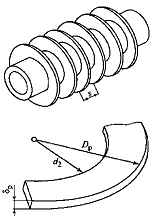
Вычислить тепловой поток с 1 п.м. длины стальных труб d2 × δ = 32 × 5 мм водяного экономайзера парогенератора для двух вариантов: а) экономайзер гладкотрубный; б) наружная поверхность труб с круглыми ребрами, внешний диаметр которых Dр = 58 мм, толщина δр = 1,2 мм. Шаг между ребрами s = 4,8 мм. В обоих вариантах средняя температура дымовых газов 450 ℃, а воды в трубах 270 ℃; коэффициент теплоотдачи от внутренней поверхности труб к воде 5200 Вт/(м2 ∙ К). Коэффициент теплоотдачи со стороны дымовых газов: в первом варианте 115 Вт/(м2 ∙ К); во втором варианте коэффициент теплоотдачи как на ребрах, так и на гладкой межреберной поверхности трубы составляет 85 Вт/(м2 ∙ К).
Решение (pdf) Решение (docx)Задача 1.38
Цена - 100 руб. (pdf) - 120 руб. (word)
Температура протекающего по трубе горячего газа измеряется термопреобразователем, который помещен в чехол. Чехол представляет собой медную трубку наружным диаметром d = 3 мм и толщиной стенки δ = 0,5 мм. Длина чехла l = 70 мм. Оцените погрешность измерения температуры газа, возникающую из-за отвода теплоты по стенке чехла к месту его крепления на трубе. Известно, что термопреобразователь дает значение tl = 300 °С, а температура в месте крепления чехла t0 = 200 °С. Коэффициент теплоотдачи от потока воздуха к чехлу α = 50 Вт/(м2 ∙ К).
Решение (pdf) Решение (docx)Задача 1.39
Цена - 100 руб. (pdf) - 120 руб. (word)
Одно основание стержня квадратного сечения 20 × 20 мм поддерживается при температуре 200 °С. Температура другого основания 65,1 °С. Температура окружающей среды равна –5 °С. Длина стержня и коэффициент теплопроводности соответственно равны 200 мм и 50 Вт/(м ∙ К). Чему равен коэффициент теплоотдачи?
Решение (pdf) Решение (docx)Задача 1.40
Цена - 100 руб. (pdf) - 120 руб. (word)
При каком значении α коэффициент эффективности плоского прямого ребра будет равен 0,34, если для ребра λ = 15 Вт/(м ∙ К); δ = 3,6 мм; l = 48 мм?
Решение (pdf) Решение (docx)Задача 1.42
Цена - 100 руб. (pdf) - 120 руб. (word)
Для плоского прямого ребра известно: t0 = 100 ℃; tж = 20 ℃; tребра = 77,6 ℃. Найти Q’/Q, где Q – тепловой поток для всего ребра; Q’ – для его половины (отсчет от основания ребра).
Решение (pdf) Решение (docx)Задача 1.43
Цена - 100 руб. (pdf) - 120 руб. (word)
Дано плоское прямое ребро δ = 4 мм, δ = 20 Вт/(м∙К); α = 12 Вт/(м∙К). На свободном конце ребра tx = l = 52,4 °С, а при x = l/2 tx = l/ 2 = 63,0. Ребро омывается жидкостью с tж = 10 °С. Найти длину ребра.
Решение (pdf) Решение (docx)Задача 1.44
Цена - 100 руб. (pdf) - 120 руб. (word)
Падение напряжения на нихромовом стержне d = 5 мм и l = 400 мм составляет ΔU = 10 В. Стержень находится в кипящей воде р = 6,18∙105 Па), а коэффициент теплоотдачи с его поверхности α = 38 000 Вт/(м2∙К). Вычислить мощность внутренних источников тепла, плотность теплового потока и линейную плотность теплового потока на поверхности стержня, температуры на его оси и поверхности. Принять для нихрома λ = 15 Вт/(м∙К), ρэл = 1,2∙10–6 Ом∙м
Решение (pdf) Решение (docx)Задача 1.45
Цена - 100 руб. (pdf) - 120 руб. (word)
Вычислить допустимую силу тока и температуру на поверхности стальной электрической шины прямоугольного сечения ab = 100 × 4 мм, установленной на ребро, если при температуре окружающего воздуха tж = 30 °С максимальная температура не должна превышать 70 °С. Коэффициент теплопроводности стали λ = 40 Вт/(м∙К), а удельное электрическое сопротивление ρэл = 0,176 Ом∙мм2/м. Теплоотдачу с боковых поверхностей шины принять α = 7 Вт/(м2∙К). Как изменится допустимый ток для шины, если при неизменной площади поперечного сечения ей придать форму круглого стержня? Изменится ли температура поверхности такой шины? (Другие условия неизменны.)
Решение (pdf) Решение (docx)Задача 1.47
Цена - 100 руб. (pdf) - 120 руб. (word)
Найти распределение температуры в цилиндрическом тепловыделяющем элементе реактора, состоящем из топливного сердечника диоксида урана UO2 диаметром d1 = 11 мм с мощностью внутренних источников qv = 3,3 ∙108 Вт/м3 и оболочки из циркония d3 х δ = 13,8 х 1,0 мм. Зазор между сердечником и оболочкой заполнен гелием, а наружная поверхность оболочки омывается водой при tж = 290 °C. Коэффициент теплоотдачи к воде α = 40000 Вт/(м2 ∙К), a коэффициенты теплопроводности диоксида урана, гелия и циркония 3; 0,3 и 20 Вт/(м ∙ К) соответственно. По результатам расчета построить график.
Решение (pdf) Решение (docx)
ГЛАВА 2. НЕСТАЦИОНАРНАЯ ТЕПЛОПРОВОДНОСТЬ
Задача 2.1
Задача 2.1
Цена - 100 руб. (pdf) - 120 руб. (word)
Определить число Био для безграничной пластины, если известно, что ее внутреннее термическое сопротивление меньше внешнего в 10 раз. Какой толщины эта пластина, если коэффициент температуропроводности, теплоемкость и плотность материала составляют 7 · 10–6 м2/с; 0,45 кДж/(кг · К) и 7940 кг/м3 соответственно. Коэффициент теплоотдачи α = 50 Вт/(м2 · К).
Решение (pdf) Решение (docx)Задача 2.2
Цена - 100 руб. (pdf) - 120 руб. (word)
Пластина толщиной 2δ0 = 20 мм, нагретая до t0 = 150 °С, помещена в воздушную среду для охлаждения. Tемпература воздуха tж = 20 °С. Коэффициенты теплопроводности и температуропроводности равны соответственно λ = 0,175 Вт/(м · К) и a = 0,833 · 10–7 м2/с. Коэффициент теплоотдачи от поверхности пластины к воздуху α = 70 Вт/(м2 · К). Определить температуры в трех точках: x = 0; x = 0,5 · δ0; x = δ0 в момент времени τ = 20 мин.
Решение (pdf) Решение (docx)Задача 2.3
Цена - 100 руб. (pdf) - 120 руб. (word)
Бетонная плита с размерами 3 × 5 × 0,3 м. и начальной температурой 90 °С в вертикальном положении охлаждается на открытом воздухе (tж = –10 °С). Определить температуру в средней плоскости плиты и на ее поверхности через 3,3 ч после начала охлаждения, если значения коэффициентов теплопроводности λ, теплоемкости c и плотности ρ для бетона составляют 1,28 Вт/(м · К), 0,84 кДж/(кг · К) и 2000 кг/м3 соответственно. Коэффициент теплоотдачи α с поверхности к воздуху принять равным 15 Вт/(м2 · К). Вычислив температуру еще хотя бы в одной промежуточной точке, построить график распределения температуры по толщине плиты.
Решение (pdf) Решение (docx)Задача 2.17
Цена - 100 руб. (pdf) - 120 руб. (word)
Опорная бетонная колонна фронтона здания имеет квадратное сечение 500 × 500 мм и высоту 5 м. Вычислить температуру на продольной оси колонны через τ = 7 ч после резкого похолодания окружающего воздуха от +10 °С до –10 °С, если коэффициент теплоотдачи с ее поверхности составляет α = 15,4 Вт/(м2 ∙ К). Для бетона λ = 1,28 Вт/(м ∙ К), а = 7,62 ∙ 10−7 м2/с. Через какое время температура в заданной точке понизится до 0 °С?
Решение (pdf) Решение (docx)
ГЛАВА 3. СВОБОДНАЯ КОНВЕКЦИЯ
Задача 3.1
Цена - 100 руб. (pdf) - 120 руб. (word)
Вертикально расположенная электрошина прямоугольного сечения 100 × 3 мм охлаждается свободным потоком воздуха с температурой t∞ = 20 °С. Рассчитать температуру шины на расстоянии 20 и 50 мм от нижней кромки при условии, что по шине снизу вверх пропускается электрический ток I = 500 А. Удельное электрическое сопротивление материала шины ρэл = 1,3 х 10–7 Ом ∙ м.
Решение (pdf) Решение (docx)Задача 3.2
Цена - 100 руб. (pdf) - 120 руб. (word)
Определить, при каком расположении плиты (горизонтальном или вертикальном) с размерами а × b = 3 × 3 м тепловой поток на поверхности будет больше, если известно, что температура теплоотдающей поверхности плиты tс = 100 °С, температура окружающего воздуха вдали от плиты t∞ = 20 °C. При горизонтальном расположении плиты теплоотдающая поверхность обращена вверх.
Решение (pdf) Решение (docx)Задача 3.3
Цена - 100 руб. (pdf) - 120 руб. (word)
Определить, при каком расположении плиты (горизонтальном или вертикальном) с размерами a × b = 0,4 × 10 м. тепловой поток на поверхности будет минимальным тепловой поток на поверхности будет минимальным, если известно, что температура теплоотдающей поверхности плиты tс = 100 °С, температура окружающего воздуха t∞ = 20 °С. При вертикальном расположении в качестве основания плиты рассмотреть меньшую (а = 0,4 м) и большую (b = 10 м) стороны. При горизонтальном расположении плиты теплоотдающая поверхность обращена вверх.
Решение (pdf) Решение (docx)Задача 3.19
Цена - 100 руб. (pdf) - 120 руб. (word)
Для интенсификации теплоотдачи при свободной конвекции на вертикальных высоких ребрах используется метод конструирования прерывистой развитой поверхности («цепочки» ребер). Рассчитать, на сколько отрезков n необходимо разбить ребро высотой H = 2 м, имеющее постоянную температуру tс = 100 °С и охлаждаемое в спокойном воздухе с температурой t∞ = 20 °С, чтобы общий тепловой поток с ребра увеличился в 1,9 раза. (Разбиение высокого ребра на «цепочку» ребер необходимо выполнить таким образом, чтобы максимально исключить тепловое влияние нижерасположенных ребер «цепочки» на вышерасположенные.)
Решение (pdf) Решение (docx)Задача 3.23
Цена - 100 руб. (pdf) - 120 руб. (word)
Пластина высотой H = 100 мм, находящаяся в воздухе с температурой t∞ = 20 °С, нагревается электрическим током до установления постоянной плотности теплового потока q = 100 Вт/м2. Найти максимальную и среднюю температуру поверхности пластины при свободноконвективном движении воздуха около нее.
Решение (pdf) Решение (docx)Задача 3.24
Цена - 100 руб. (pdf) - 120 руб. (word)
Тонкий лист нержавеющей стали толщиной δ = 0,02 мм, шириной b = 150 мм. и высотой H = 600 мм. с удельным электрическим сопротивлением ρэл = 0,13 ∙ 10–6 Ом ∙ м находится в воде. Он нагревается электрическим током до получения постоянной плотности теплового потока qс = 200 Вт/м2. Определить требуемый для этого ток, среднюю температуру стенки, среднюю скорость движения воды и толщину пограничного слоя на высоте Н = 300 мм. Температура воды вдали от поверхности t∞ = 30 °С. Движение воды принять ламинарным.
Решение (pdf) Решение (docx)
ГЛАВА 4. ВЫНУЖДЕННОЕ ВНЕШНЕЕ ОБТЕКАНИЕ
Задача 4.1
Цена - 100 руб. (pdf) - 120 руб. (word)
Тонкая пластина омывается потоком воздуха со скоростью w∞ = 2 м/с при температуре t∞ = 50 °С. Определить в сечениях x1 = 0,2 м и x2 = 0,3 м характер течения в пограничном слое и найти: а) толщины динамического пограничного слоя; б) локальные коэффициенты теплоотдачи для случая tc = const; в) средний коэффициент теплоотдачи на длине х = 0,5 м.
Решение (pdf) Решение (docx)Задача 4.2
Цена - 100 руб. (pdf) - 120 руб. (word)
Найдите толщины динамического и теплового пограничных слоев в точке х = 1 м при обтекании пластины воздухом (t∞ = 30 °С, w∞ = 5 м/с). Температура пластины tс = 10 °С. Определите коэффициент теплоотдачи α в данной точке, а также средний коэффициент теплоотдачи для участка пластины 0 ≤ х ≤ 1 м.
Решение (pdf) Решение (docx)Задача 4.3
Цена - 100 руб. (pdf) - 120 руб. (word)
Найдите толщины динамического и теплового пограничных слоев в точке х = 1 м при обтекании пластины водой (t∞ = 30 °С, w∞ = 0,1 м/с). Температура пластины tс = 10 °С. Определите коэффициент теплоотдачи α в данной точке, а также средний коэффициент теплоотдачи для участка пластины 0 ≤ х ≤ 1 м.
Решение (pdf) Решение (docx)Задача 4.4
Цена - 100 руб. (pdf) - 120 руб. (word)
Плоская стенка длиной l = 3 м и шириной b = 1,8 м омывается продольным потоком воздуха, скорость которого w∞ = 5 м/с и температура t∞ = 30 °С. Температура поверхности стенки tс = 250 °С (qс = const). Определить средний по длине стенки коэффициент теплоотдачи и количество тепла, отдаваемое воздуху.
Решение (pdf) Решение (docx)Задача 4.5
Цена - 100 руб. (pdf) - 120 руб. (word)
Пластина длиной l = 2 м и шириной b = 1 м омывается продольным потоком жидкости с t∞ = 20 °C. Вычислить максимальное значение толщины ламинарного пограничного слоя, толщину пограничного слоя на конце пластины и полное сопротивление пластины в изотермических условиях для трех случаев: а) поток воздуха, w∞ = 3 м/с; б) поток масла МК, w∞ = 1 м/с; в) поток воды, w∞ = 0,5 м/с.
Решение (pdf) Решение (docx)Задача 4.6
Цена - 100 руб. (pdf) - 120 руб. (word)
Электрическая шина, выполненная из стали с размерами l × b × δ = 5 × 0,05 × 0,001 м. (ρэл = 0,13 ∙ 10–6 Ом ∙ м) охлаждается продольным потоком воздуха с w∞ = 20 м/с и t∞ = 20 °С. По шине, вдоль ее длины, пропускается электрический ток I = 100 А. Вычислить максимальную и среднюю по поверхности шины температуры, если: а) шина обдувается вдоль ее ширины b; б) шина обдувается вдоль ее длины l.
Решение (pdf) Решение (docx)Задача 4.7
Цена - 100 руб. (pdf) - 120 руб. (word)
Тонкая пластина из нержавеющей стали обогревается электрическим током так, что qc = 386 Вт/м2. Пластина продольно обдувается воздухом (w∞ = 10 м/с и t∞ = 10 °С). Найдите температуру пластины на расстоянии х = 0,2 м. от передней кромки.
Решение (pdf) Решение (docx)Задача 4.8
Цена - 100 руб. (pdf) - 120 руб. (word)
Для охлаждения внешней поверхности электродвигателя ДА - 100L4 используются продольные прямоугольные ребра высотой l = 18 мм, шириной b = 9 мм, толщиной δ = 1,26 мм. Коэффициент теплоотдачи в межреберных каналах α = 160 Вт/(м2 ∙ К). Как изменится тепловой поток с поверхности ребер, если длину продольных прямоугольных ребер уменьшить в 2 раза, расположив на поверхности электродвигателя вместо длинных ребер «цепочку» ребер? Принять, что течение воздуха в межреберных каналах, обдуваемых вентилятором, ламинарное и теплоотдача определяется по формуле 𝑁𝑢 = 𝐶𝑅𝑒х0,522
Решение (pdf) Решение (docx)Задача 4.9
Цена - 100 руб. (pdf) - 120 руб. (word)
Для набегающего на пластину потока воздуха скорость w∞ = 200 м/с и температура t∞ = 20 °С. Рассчитайте плотность теплового потока qc в точке х = 35 мм при температуре пластины: а) tс = 36,8 °С; б) tс = 25 °С; в) tс = 40 °С.
Решение (pdf) Решение (docx)Задача 4.10
Цена - 100 руб. (pdf) - 120 руб. (word)
Вычислить среднюю плотность теплового потока на боковой поверхности вагона - холодильника при движении поезда со скоростью w∞ = 80 км/ч, если известно, что температура наружного воздуха t∞ = 25 °C, температура внутренней поверхности стенки вагона tc = 0 °С. Принять термическое сопротивление теплопроводности стенки вагона δ/λ = 0,3 (м2 ∙ К)/Вт, а длину стенки вагона l = 10 м.
Решение (pdf) Решение (docx)Задача 4.11
Цена - 100 руб. (pdf) - 120 руб. (word)
По круглой вертикальной трубе, выполненной из меди и имеющей размеры d2/d1 = 100/90 мм и l = 1 м, прокачивают горячую воду с tж = 90 ℃. На наружной поверхности трубы равномерно установлено 10 продольных ребер прямоугольного сечения. Толщина ребер δ = 3 мм, длина lр = 50 мм. Оценить тепловой поток с оребренной поверхности трубы к окружающему воздуху (t∞ = 20 ℃) для двух случаев: а) окружающий трубу воздух находится в спокойном состоянии; б) оребренная труба обдувается в продольном направлении вентилятором, w∞ = 7 м/с.
Указание. При решении задачи термическим сопротивлением теплоотдачи к внутренней поверхности трубы пренебречь.
Задача 4.12
Цена - 100 руб. (pdf) - 120 руб. (word)
Плоская пластина омывается турбулентным потоком воды с t∞ = 50 ℃. Средняя температура поверхности пластины tс = 70 ℃. Как изменится коэффициент теплоотдачи и чему будет равна температура поверхности в случае изменения направления теплового потока (т.е. в случае охлаждения потока воды), если зависимость вязкости от температуры для воды приближенно может быть принята μ = 0,0125 t-0,8 Па ∙ с.
Решение (pdf) Решение (docx)Задача 4.13
Цена - 100 руб. (pdf) - 120 руб. (word)
Пластина длиной l = 1,5 м продольно обтекается потоком воздуха (w∞ = 50 м/с, t∞ = 8 °С, p∞ = 0,202 МПа). Из-за наличия перед ней турбулизирующей решетки течение в пограничном слое турбулентное. Температура пластины tc = 12 °С. Найдите средний коэффициент теплоотдачи, а также толщины пограничного слоя и вязкого подслоя на задней кромке пластины.
Решение (pdf) Решение (docx)Задача 4.14
Цена - 100 руб. (pdf) - 120 руб. (word)
Нагретая пластина длиной l = 2 м продольно омывается потоком воды. Скорость воды w∞ = 0,5 м/с, и ее температура t∞ = 180 ℃. Постройте графики распределения теплоотдачи от поверхности пластины к воде для двух случаев: а) малая степень турбулентности потока воды (ε ≈ 0,08 %); б) большая степень турбулентности (ε ≈ 0,3 %). Найдите также αср – средний коэффициент теплоотдачи. Считайте, что разность температур пластины и воды мала, в расчете теплоотдачи изменением физических свойств воды с изменением температуры можно пренебречь.
Решение (pdf) Решение (docx)Задача 4.15
Цена - 100 руб. (pdf) - 120 руб. (word)
Ртутный термометр для измерения температуры потока воздуха, движущегося в трубе со скоростью w = 0,5 м/с, расположен под углом φ = 60° к направлению потока. Среднемассовая температура воздуха в трубе tж = 100 ℃, температура термометра в месте, где он проходит через стенку трубы, t0 = 60 ℃. Наружный диаметр термометра d = 5 мм, толщина стенок стеклянной колбы δ = 1 мм. Оценить погрешность в показаниях термометра за счет отвода теплоты вдоль его стенок, если длина погруженной части термометра в поток l = 50 мм.
Решение (pdf) Решение (docx)Задача 4.16
Цена - 100 руб. (pdf) - 120 руб. (word)
Электропровод из алюминия диаметром d = 4 мм и длиной l = 0,7 м, ρэл = 2,66 ∙ 10–8 Ом∙м, по которому пропускается ток I = 100 А, обдувается потоком воздуха с w∞ = 6 м/c и t∞ = 20 °C. Определить среднюю по длине температуру электропровода для двух случаев: а) провод обдувается в поперечном направлении; б) провод обдувается в продольном направлении.
Решение (pdf) Решение (docx)Задача 4.17
Цена - 100 руб. (pdf) - 120 руб. (word)
Электронагреватель в виде трубы диаметром d = 15 мм и длиной l = 1 м обдувается поперечным потоком воздуха, температура которого t∞ = 20 °C. Определить скорость движения воздуха, если известно, что мощность нагревателя Q = 523,4 Вт, а температура стенки не должна превышать tс = 150 °С.
Решение (pdf) Решение (docx)Задача 4.18
Цена - 100 руб. (pdf) - 120 руб. (word)
В теплообменнике «газ — газ» разреженный пучок труб омывается дымовыми газами. Температура набегающего потока tж1 = 800 °С, а скорость w∞ = 15 м/с. Для газов, протекающих внутри труб, tж2 = 300 °С и α2 = 90 Вт/(м2 ∙ К). Трубы диаметром и толщиной стенки d2 × δ = 32 × 5 мм. изготовлены из стали 12Х1МФ, допустимая рабочая температура которой 550 °С. Найдите среднюю температуру наружной поверхности трубы и температуру в первой критической (лобовой) точке и сопоставьте найденные значения с допустимой рабочей температурой стали.
Решение (pdf) Решение (docx)Задача 4.19
Цена - 100 руб. (pdf) - 120 руб. (word)
Вертикальная труба d = 100 мм и высотой h = 0,5 м находится в спокойном воздухе с t∞ = 20 °С. Температура стенки трубы tс = 120 °С. Определить скорость вынужденного движения воздуха вдоль поверхности трубы, если известно, что при вынужденном продольном омывании трубы тепловой поток с поверхности остается таким же, как и в случае свободной конвекции.
Решение (pdf) Решение (docx)Задача 4.20
Цена - 100 руб. (pdf) - 120 руб. (word)
Труба наружным диаметром d = 20 мм обтекается поперечным потоком горячего трансформаторного масла с температурой t∞ = 100 °C и скоростью w∞ = 1 м/с. Плотность теплового потока на поверхности трубы поддерживается равной q = 7000 Вт/м2 и направлена от масла к стенке. Под каким углом к поверхности трубы следует направить поток масла, чтобы температура поверхности понизилась на Δt = 3 °С?
Решение (pdf) Решение (docx)Задача 4.21
Цена - 100 руб. (pdf) - 120 руб. (word)
Найти соотношение между средними коэффициентами теплоотдачи для третьего ряда труб по ходу воздуха двух воздухоподогревателей, конструктивно выполненных в виде трубных пучков: а) с шахматным расположением труб; б) с коридорным расположением труб. Оба пучка обтекаются поперечным потоком воздуха с одинаковой средней температурой и скоростью в узком сечении пучка. Диаметры труб в обоих пучках одинаковы, шаги труб в пучках также одинаковы, причем s1 > s2.
Решение (pdf) Решение (docx)Задача 4.22
Цена - 100 руб. (pdf) - 120 руб. (word)
Как изменится средний коэффициент теплоотдачи пятого ряда труб воздушных подогревателей, конструктивно выполненных в виде трубных пучков с шахматным расположением труб, если диаметр трубы в пучке уменьшить в 3 раза при условии постоянства расхода газа, поперечного s1 и продольного s2 шагов труб в пучке. Принять s1 = 2d.
Решение (pdf) Решение (docx)Задача 4.23
Цена - 100 руб. (pdf) - 120 руб. (word)
Как изменится средний коэффициент теплоотдачи пятого ряда труб воздушных подогревателей, конструктивно выполненных в виде трубных пучков с коридорным расположением труб, если диаметр трубы в пучке уменьшить в 3 раза при условии постоянства расхода газа, поперечного s1 и продольного s2 шагов труб в пучке. Принять s1 = 2d.
Решение (pdf) Решение (docx)Задача 4.24
Цена - 100 руб. (pdf) - 120 руб. (word)
Радиатор охлаждения автомобиля выполнен в виде двухрядного коридорного пучка, скомпонованного из латунных трубок с шагами s1 = s2 = 1,5d. Диаметр трубок d = 5 х 0,25 мм и длина l = 0,4 м. Количество трубок в каждом ряду равно 40. До какой температуры охлаждается рабочая жидкость (вода) в радиаторе, если известно, что скорость автомобиля w = 100 км/ч, а температура воды на входе в радиатор tж1 = 100 °С. Скорость движения воды в трубках wвод = 0,1 м/с. Температура окружающего воздуха tвоз = 20 °С.
Решение (pdf) Решение (docx)Задача 4.25
Цена - 100 руб. (pdf) - 120 руб. (word)
Найти соотношение между средними коэффициентами теплоотдачи и мощностями, потребными для прокачки воздуха через трубный пучок для двух десятирядных воздухоподогревателей, конструктивно выполненных в виде трубных пучков: а) с шахматным расположением труб; б) с коридорным расположением труб. Оба пучка обтекаются поперечным потоком воздуха с одинаковым расходом, средней температурой и одинаковой скоростью в узком сечении пучка, равной w = 8 м/с. Диаметры труб в обоих пучках одинаковы и равны d = 50 мм. Относительные шаги также одинаковы: s1/d × s2/d = 1,9 × 1,3.
Решение (pdf) Решение (docx)Задача 4.26
Цена - 100 руб. (pdf) - 120 руб. (word)
Найдите средний коэффициент теплоотдачи при поперечном обтекании дымовыми газами пакета труб экономайзера парового котла. Экономайзер собран из плоских змеевиков с шахматным расположением труб диаметром и толщиной стенки 32 × 6 мм, причем s1/d = 2,4, a s2/d = 1,8, а число рядов равно 40. Скорость газов в узком сечении wуз = 14 м/с. Их температура на входе в пакет труб 520 °С, а на выходе из него 380 °С.
Решение (pdf) Решение (docx)Задача 4.27
Цена - 100 руб. (pdf) - 120 руб. (word)
Найдите средний коэффициент теплоотдачи при поперечном обтекании дымовыми газами пакета труб экономайзера парового котла. Экономайзер собран из плоских змеевиков с коридорным расположением труб диаметром и толщиной стенки 32 × 6 мм, причем s1/d = 2,4, a s2/d = 1,8, а число рядов равно 40. Скорость газов в узком сечении wуз = 14 м/с. Их температура на входе в пакет труб 520 °С, а на выходе из него 380 °С.
Решение (pdf) Решение (docx)Задача 4.28
Цена - 100 руб. (pdf) - 120 руб. (word)
Рассчитать коэффициент теплопередачи и аэродинамическое сопротивление в пятирядном гладкотрубном пароперегревателе, обтекаемом поперечным потоком дымовых газов. Стальные трубы, из которых выполнен пароперегреватель, имеют диаметр d = 40 мм и расположены в коридорном порядке. Относительный поперечный и продольный шаги труб в пучке равны соответственно s1/d = 2,5, s2/d = 2. Средняя скорость потока газа в узком сечении пучка w = 10 м/с. Температура газа перед пучком tж1 = 1100° С, за пучком tж2 = 900 °С.
Указание. При решении задачи не учитывать радиационную составляющую коэффициента теплоотдачи и пренебречь термическим сопротивлением теплоотдачи от пара к стенке. Термическое сопротивление теплопроводности стенки трубы принять равным R = 2 ∙ 10–4 (м2 ∙ К)/Вт.
Задача 4.29
Цена - 100 руб. (pdf) - 120 руб. (word)
Как изменятся коэффициент теплопередачи и аэродинамическое сопротивление в задаче 4.28, если увеличить компактность трубного пучка за счет уменьшения поперечного шага до значения s1/d = 2,0 при (s1/d – d)/(s’2/d – d) = idem, s’2 – диагональный шаг труб в пучке.
Решение (pdf) Решение (docx)Задача 4.30
Цена - 100 руб. (pdf) - 120 руб. (word)
Экономайзер котельной установки изготовлен из стальных гладких труб диаметром d2/d1 = 37/30 мм, расположенных в шахматном порядке с относительным поперечным и продольным шагом соответственно s1/d = 2,0, s2/d = 1,5. Число поперечных рядов труб по ходу газа z = 6. Температура дымовых газов на входе в экономайзер и выходе из него соответственно tж1 = 600 ℃, tж2 = 400 ℃, а скорость в узком сечении пучка w = 12 м/с. Какой общей длины должны быть трубы, если известно, что тепловой поток, передаваемый воде, протекающей внутри труб, Q = 32000 кВт, а температура наружной стенки трубы tс = 230 ℃. Определить также аэродинамическое сопротивления экономайзера.
Решение (pdf) Решение (docx)
